Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Stoke's law (for highly viscous liquids)
Stoke's law (for highly viscous liquids)
When a body falls through a highly viscous liquid, it drags the
layer of the liquid immediately in contact with it. This results in a relative
motion between the different layers of the liquid. As a result of this, the
falling body experiences a viscous force F.
Stoke performed many experiments on the motion of small spherical bodies in
different fluids and concluded that the viscous force F acting on the spherical body depends on
(i)
Coefficient of viscosity η of the liquid
(ii) Radius a of the sphere and
(iii)
Velocity v of the spherical body. Dimensionally it can be proved
that
F = k ηav
Experimentally Stoke found
that
k = 6π
F = 6π ηav
This is Stoke's law.
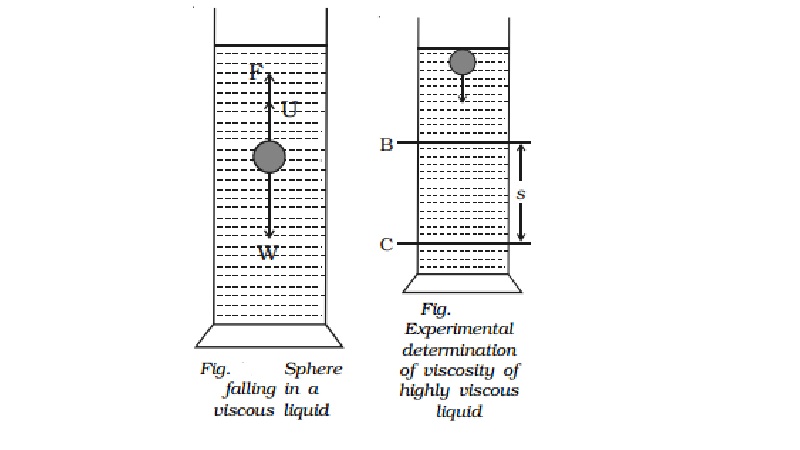
Expression for terminal velocity
Consider a metallic sphere of
radius 'a' and density ρ to fall under gravity in a liquid of density σ. The
viscous force F acting on the metallic sphere increases as its velocity
increases. A stage is reached when the weight W of the sphere becomes equal to
the sum of the upward viscous force F and the upward thrust U due to buoyancy
(Fig.). Now, there isno net force acting on the sphere and it moves down with a
constant velocity v called terminal velocity.
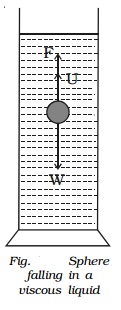
W - F - U = O ...(1)
Terminal velocity of a body
is defined as the constant velocity acquired by a body while falling through a
viscous liquid.
From (1), W = F + U ….. ...(2)
According to Stoke's law, the
viscous force F is given by F = 6πηav.
The buoyant force U = Weight
of liquid displaced by the sphere
= 4/3 πa3σ g
The weight of the sphere W =
4/3 πa3ρg
Substituting in equation (2)
4/3 πa ρg = 6π ηav +4/3 πa3
σ g
∴ v = 2 a2(ρ- σ)g / 9η
Experimental determination of viscosity of highly viscous liquids
The coefficient of highly
viscous liquid like castoroil can be determined by Stoke's method. The
experimental liquid is taken in a tall, wide jar. Two marking B and C are
marked as shown in Fig.. A steel ball is gently dropped in the jar.
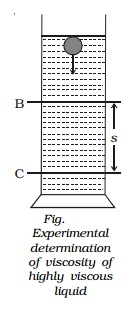
The marking B is made well
below the free surface of the liquid so that by the time ball reaches B, it
would have acquired terminal velocity v.
When the ball crosses B, a
stopwatch is switched on and the time taken t to reach C is noted. If the
distance BC is s, then terminal velocity v =s / t .
The expression for terminal velocity
is
v = 2 a2(ρ- σ)g / 9η
η = 2/9 . 2 a2(ρ- σ)g . t/s
Knowing a, ρ and σ, the value
of η of the liquid is determined.
Application of Stoke's law
Falling of rain drops: When the water drops are small in size,
their terminal velocities are small. Therefore they remain suspended in air in
the form of clouds. But as the drops combine and grow in size, their terminal
velocities increases because v α a2. Hence
they start falling as rain.
Related Topics