Refraction at a spherical surface

Refraction at a spherical surface

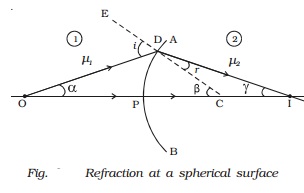
Let us consider a portion of a spherical surface AB separating two media having refracting indices ?₁ and ?₂ (Fig. ). This is symmetrical about an axis passing through the centre C and cuts the surface at P.

The point P is called the pole of the surface. Let R be the radius of curvature of the surface.

Consider a point object O on the axis in the first medium. Consider two rays OP and OD originating from O. The ray OP falls normally on AB and goes into the second medium, undeviated. The ray OD falls at D very close to P. After refraction, it meets at the point I on the axis, where the image is formed. CE is the normal drawn to the point D. Let i and r be the angle of incidence and refraction respectively.

Let angle DOP = α, angle DCP =  β, Angle DIC = γ

Since D is close to P, the angles α, β and γ are all small. From the Fig.

tan α = DP/PO

tan β = DP/PO

tan γ = DP/PI

α = DP/PO

β = DP/PO

γ = DP/PI

From the ∆ODC, i = α + β   ??..(1)

From the ∆DCI, β = r + γ or r = β ? γ    ???(2)

From Snell?s Law, ?₂/ ?₁ = sin i/ sin r and for small angles of i and r, we can write, ?₁  i = ?₂r ...(3)

we get ?₁  (α + β) = ?₂  (β − γ) or ?₁ α + ?₂ γ = (?₂ - ?₁ )β         ????(4)

Substituting the values of α, β and γ in equation (4)

?₁(DP/PO) + ?₂ (DP/PI) = (?₂ - ?₁) . DP/PC

?₁/PO + ?₂/PI = ( ?₂ - ?₁ ) /PC

As the incident ray comes from left to right, we choose this direction as the positive direction of the axis. Therefore u is negative, whereas v and R are positive substitute PO = ?u PI = +v and PC = +R in equation (5),

( ?₁ / -u ) + (?₂/v) = (?₂- ?₁)/R

(?₂/v) - ( ?₁ / u ) +  = (?₂- ?₁)/R          ???.(6)

Equation (6) represents the general equation for refraction at a spherical surface.

If the first medium is air and the second medium is of refractive index ?, then

(? / v) ? ( 1/u) = (? -1)/R