Refraction of light

Refraction of light

When a ray of light travels from one transparent medium into another medium, it bends while crossing the interface, separating the two media. This phenomenon is called refraction.

Image formation by spherical lenses is due to the phenomenon of refraction. The laws of refraction at a plane surface are equally true for refraction at curved surfaces also. While deriving the expressions for refraction at spherical surfaces, we make the following assumptions.

(i) The incident light is assumed to be monochromatic and

(ii)                  the incident pencil of light rays is very narrow and close to the principal axis.

1 Cartesian sign convention

The sign convention followed in the spherical mirror is also applicable to refraction at spherical surface. In addition to this two more sign conventions to be introduced which are:

(i)                     The power of a converging lens is positive and that of a diverging lens is negative.

(ii)                  The refractive index of a medium is always said to be positive. If two refractions are involved, the difference in their refractive index is also taken as positive.

2 Refraction at a spherical surface

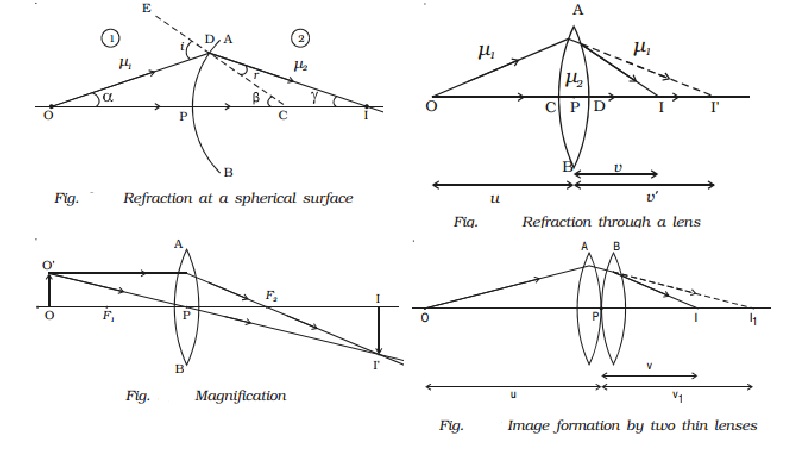
Let us consider a portion of a spherical surface AB separating two media having refracting indices ?₁ and ?₂ (Fig. ). This is symmetrical about an axis passing through the centre C and cuts the surface at P.

The point P is called the pole of the surface. Let R be the radius of curvature of the surface.

Consider a point object O on the axis in the first medium. Consider two rays OP and OD originating from O. The ray OP falls normally on AB and goes into the second medium, undeviated. The ray OD falls at D very close to P. After refraction, it meets at the point I on the axis, where the image is formed. CE is the normal drawn to the point D. Let i and r be the angle of incidence and refraction respectively.

Let angle DOP = α, angle DCP =  β, Angle DIC = γ

Since D is close to P, the angles α, β and γ are all small. From the Fig.

tan α = DP/PO

tan β = DP/PO

tan γ = DP/PI

α = DP/PO

β = DP/PO

γ = DP/PI

From the ∆ODC, i = α + β   ??..(1)

From the ∆DCI, β = r + γ or r = β ? γ    ???(2)

From Snell?s Law, ?₂/ ?₁ = sin i/ sin r and for small angles of i and r, we can write, ?₁  i = ?₂r ...(3)

we get ?₁  (α + β) = ?₂  (β − γ) or ?₁ α + ?₂ γ = (?₂ - ?₁ )β         ????(4)

Substituting the values of α, β and γ in equation (4)

?₁(DP/PO) + ?₂ (DP/PI) = (?₂ - ?₁) . DP/PC

?₁/PO + ?₂/PI = ( ?₂ - ?₁ ) /PC

As the incident ray comes from left to right, we choose this direction as the positive direction of the axis. Therefore u is negative, whereas v and R are positive substitute PO = ?u PI = +v and PC = +R in equation (5),

( ?₁ / -u ) + (?₂/v) = (?₂- ?₁)/R

(?₂/v) - ( ?₁ / u ) +  = (?₂- ?₁)/R          ???.(6)

Equation (6) represents the general equation for refraction at a spherical surface.

If the first medium is air and the second medium is of refractive index ?, then

(? / v) ? ( 1/u) = (? -1)/R

.3 Refraction through thin lenses

A lens is one of the most familiar optical devices. A lens is made of a transparent material bounded by two spherical surfaces. If the distance between the surfaces of a lens is very small, then it is a thin lens.

As there are two spherical surfaces, there are two centres of curvature C₁ and C₂ and correspondingly two radii of curvature R₁ and R₂. The line joining C₁ and C₂ is called the principal axis of the lens. The centre P of the thin lens which lies on the principal aixs is called the optic centre.

4 Lens maker?s formula and lens formula

Let us consider a thin lens made up of a medium of refractive index ?₂ placed in a medium of refractive index ?₁. Let R₁ and R₂ be the radii of curvature of two spherical surfaces ACB and ADB respectively and P be the optic centre.

Consider a point object O on the principal axis. The ray OP falls normally on the spherical surface and goes through the lens undeviated. The ray OA falls at A very close to P. After refraction at the surface ACB the image is formed at I′. Before it does so, it is again refracted by the surface ADB. Therefore the final image is formed at I as shown in Fig.

The general equation for the refraction at a spherical surface is given by

( ?₂/v ) ? (?₁/u) = (?₂-?₁)/R       ????.(1)

For the refracting surface ACB, from equation (1) we write

?₂/v?  - ?₁/u  = (?₂-?₁)/R₁  ????..(2)

The image I′ acts as a virtual object for the surface ADB and the final image is formed at I. The second refraction takes place when light

travels from the medium of refractive index ?₂  to ?₁.

For the refracting surface ADB, from equation (1) and applying sign conventions, we have

?₁/v  - ?₂/v? =[ (?₂ - ?₁)(-R₂)]   ????(3)

. Adding equations (2) and (3)

?₁/v  - ?₂/u = (?₂ - ?₁ )[1/R₁  - 1/R₂]

Dividing the above equation by ?₁

1/v -1/u = [(?₂/ ?₁)-1][ 1/R₁ ? 1/R₂ ]            ???????..(4)

If the object is at infinity, the image is formed at the focus of the lens.

Thus, for u = ∞, v = f. Then the equation (4) becomes.

1/f =  [(?₂/ ?₁)-1][ 1/R₁ ? 1/R₂ ]            ???????..(5)

If the refractive index of the lens is ? and it is placed in air, ?₂  = ? and ?₁  = 1. So the equation (5) becomes

1/f =  [?-1][ 1/R₁ ? 1/R₂ ]            ???????..(6)

This is called the lens maker?s formula, because it tells what curvature will be needed to make a lens of desired focal length. This formula is true for concave lens also.

Comparing equation (4) and (5)

We get 1/v ? 1/u = 1/f              ??..(7)

which is known as the lens formula.

5 Magnification

Let us consider an object OO ′ placed on the principal axis with its height perpendicular to the principal axis as shown in Fig.  The ray OP passing through the optic centre will go undeviated. The ray O ′A parallel to the principal axis must pass through the focus F2

. The image is formed where O ′PI′ and AF2 I′ intersect. Draw a perpendicular from I′ to the principal axis. This perpendicular II ′ is

the image of OO ′.

The linear or transverse magnification is defined as the ratio of the size of the image to that of the object.

Magnification m = Size of the image / Size of the object = II?/OO? = h₂/h₁

where h₁  is the height of the object and h₂  is the height of the image.

From the similar right angled triangles OO′ P and II′ P, we have II?/OO? = PI/PO

Applying sign convention,

II′ = -h₂

OO? = +h₁

PI = +v

PO = -u

Substituting this in the above equation, we get magnification

M=-h₂/+h₁ = +v/-u

M=+ v/u

The magnification is negative for real image and positive for virtual image. In the case of a concave lens, it is always positive.

Using lens formula the equation for magnification can also be obtained as

m = h₂/h₁ = v//u = (f-v)/f = f/(f+u)

This equation is valid for both convex and concave lenses and for real and virtual images.

6 Power of a lens

Power of a lens is a measure of the degree of convergence or divergence of light falling on it. The power of a lens (P) is defined as the reciprocal of its focal length.

P=1/f

The unit of power is dioptre (D) : 1 D = 1 m^-1. The power of the lens is said to be 1 dioptre if the focal length of the lens is 1 metre. P is positive for converging lens and negative for diverging lens. Thus, when an optician prescribes a corrective lens of power + 0.5 D, the required lens is a convex lens of focal length + 2 m. A power of -2.0 D means a concave lens of focal length -0.5 m.

7 Combination of thin lenses in contact

Let us consider two lenses A and B of focal length  f₁  and f₂  placed in contact with each other. An object is placed at O beyond the focus of the first lens A on the common principal axis.

The lens A produces an image at I₁ . This image I₁ acts as the object for the second lens B. The final image is produced at I as shown in Fig.  Since the lenses are thin, a common optical centre P is chosen.

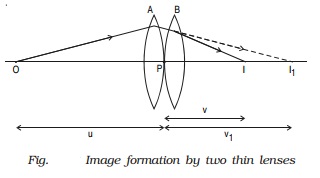
Let PO = u, object distance for the first lens (A), PI = v, final image distance and PI₁ = v₁, image distance for the first lens (A) and also object distance for second lens (B).

For the image I₁  produced by the first lens A,

1/v₁ ? 1/u = 1/f₁    ????..(1)

For the final image I, produced by the second lens B,

1/v  - 1/v₁ = 1/f_{2      ????..}(2)

Adding equations (1) and (2),

1/v ? 1/u = 1/f₁ + 1/f₂ ????..(3)

If the combination is replaced by a single lens of focal length F such that it forms the image of O at the same position I, then

1/v  - 1/u  = 1/F       ????(4)

From equations (3) and (4)

1/F = 1/f₁   +   1/f₂   ?????(5)

This F is the focal length of the equivalent lens for the combination. The derivation can be extended for several thin lenses of focal

lengths f₁, f₂, f₃  ... in contact. The effective focal length of the combination is given by

1/F = 1/f₁   +  1/f₂  +  1/f₃   + ?????..         ?..(6)

In terms of power, equation (6) can be written as

P = P₁ + P₂ + P₃ + ....                 ...(7)

Equation (7) may be stated as follows :

The power of a combination of lenses in contact is the algebraic sum of the powers of individual lenses.

The combination of lenses is generally used in the design of objectives of microscopes, cameras, telescopes and other optical instruments.