Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Lens maker's formula and lens formula and Magnification

Lens maker s formula
and lens formula
Let us consider a thin
lens made up of a medium of refractive index ?2 placed in a medium of refractive index ?1. Let R1 and R2 be the radii of curvature of two spherical surfaces ACB and ADB respectively and P be
the optic centre.
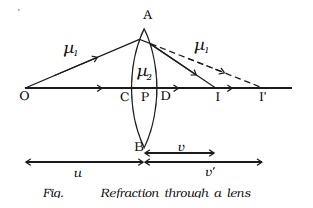
Consider a point
object O on the principal axis. The ray OP falls normally on the spherical
surface and goes through the lens undeviated. The ray OA falls at A very close
to P. After refraction at the surface ACB the image is formed at I′. Before it
does so, it is again refracted by the surface ADB. Therefore the final image is
formed at I as shown in Fig.
The general equation for
the refraction at a spherical surface is given by
( ?2/v ) ?
(?1/u) = (?2-?1)/R ????.(1)
For the refracting
surface ACB, from equation (1) we write
?2/v? - ?1/u = (?2-?1)/R1 ????..(2)
The image I′ acts as a
virtual object for the surface ADB and the final image is formed at I. The
second refraction takes place when light
travels from the
medium of refractive index ?2
to ?1.
For the refracting
surface ADB, from equation (1) and applying sign conventions, we have
?1/v - ?2/v? =[ (?2 - ?1)(-R2)] ????(3)
.
Adding equations (2)
and (3)
?1/v - ?2/u = (?2 - ?1
)[1/R1 - 1/R2]
Dividing the above
equation by ?1
1/v -1/u = [(?2/
?1)-1][ 1/R1 ? 1/R2 ] ???????..(4)
If the object is at
infinity, the image is formed at the focus of the lens.
Thus, for u = ∞, v =
f. Then the equation (4) becomes.
1/f = [(?2/ ?1)-1][ 1/R1
? 1/R2 ]
???????..(5)
If the refractive
index of the lens is ? and it is placed in air, ?2 = ? and ?1 = 1. So the equation (5) becomes
1/f = [?-1][ 1/R1 ? 1/R2 ] ???????..(6)
This is called the
lens maker?s formula, because it tells what curvature will be needed to make a
lens of desired focal length. This formula is true for concave lens also.
Comparing equation (4)
and (5)
We get 1/v ? 1/u =
1/f ??..(7)
which is known as the
lens formula.
Magnification
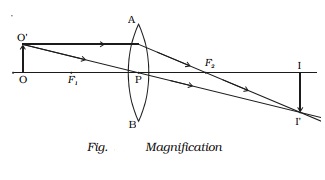
Let us consider an
object OO ′ placed on the principal axis with its height perpendicular to the
principal axis as shown in Fig. The ray
OP passing through the optic centre will go undeviated. The ray O ′A parallel to
the principal axis must pass through the focus F2
. The image is formed
where O ′PI′ and AF2 I′ intersect. Draw a perpendicular from I′ to the
principal axis. This perpendicular II ′ is
the image of OO ′.
The linear or
transverse magnification is defined as the ratio of the size of the image to
that of the object.
Magnification m = Size
of the image / Size of the object = II?/OO? = h2/h1
where h1 is the height of the object and h2 is the height of the image.
From the similar right
angled triangles OO′ P and II′ P, we have II?/OO? = PI/PO
Applying sign
convention,
II′ = -h2
OO? = +h1
PI = +v
PO = -u
Substituting this in
the above equation, we get magnification
M=-h2/+h1
= +v/-u
M=+ v/u
The magnification is
negative for real image and positive for virtual image. In the case of a
concave lens, it is always positive.
Using lens formula the
equation for magnification can also be obtained as
m = h2/h1
= v//u = (f-v)/f = f/(f+u)
Related Topics