Combination of thin lenses in contact

Power of a lens

Power of a lens is a measure of the degree of convergence or divergence of light falling on it. The power of a lens (P) is defined as the reciprocal of its focal length.

P=1/f

The unit of power is dioptre (D) : 1 D = 1 m^-1. The power of the lens is said to be 1 dioptre if the focal length of the lens is 1 metre. P is positive for converging lens and negative for diverging lens. Thus, when an optician prescribes a corrective lens of power + 0.5 D, the required lens is a convex lens of focal length + 2 m. A power of -2.0 D means a concave lens of focal length -0.5 m.

Combination of thin lenses in contact

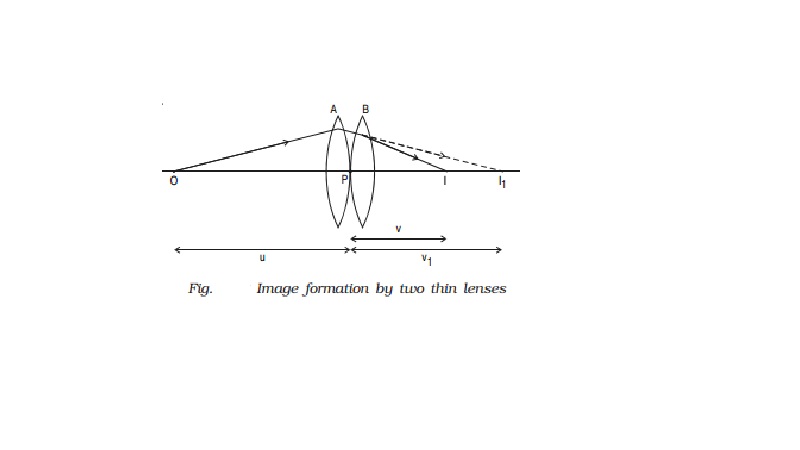
Let us consider two lenses A and B of focal length  f₁  and f₂  placed in contact with each other. An object is placed at O beyond the focus of the first lens A on the common principal axis.

The lens A produces an image at I₁ . This image I₁ acts as the object for the second lens B. The final image is produced at I as shown in Fig.  Since the lenses are thin, a common optical centre P is chosen.

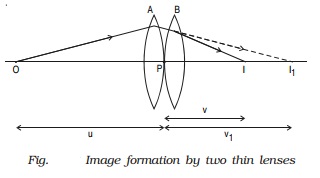
Let PO = u, object distance for the first lens (A), PI = v, final image distance and PI₁ = v₁, image distance for the first lens (A) and also object distance for second lens (B).

For the image I₁  produced by the first lens A,

1/v₁ ? 1/u = 1/f₁    ????..(1)

For the final image I, produced by the second lens B,

1/v  - 1/v₁ = 1/f_{2      ????..}(2)

Adding equations (1) and (2),

1/v ? 1/u = 1/f₁ + 1/f₂ ????..(3)

If the combination is replaced by a single lens of focal length F such that it forms the image of O at the same position I, then

1/v  - 1/u  = 1/F       ????(4)

From equations (3) and (4)

1/F = 1/f₁   +   1/f₂   ?????(5)

This F is the focal length of the equivalent lens for the combination. The derivation can be extended for several thin lenses of focal

lengths f₁, f₂, f₃  ... in contact. The effective focal length of the combination is given by

1/F = 1/f₁   +  1/f₂  +  1/f₃   + ?????..         ?..(6)

In terms of power, equation (6) can be written as

P = P₁ + P₂ + P₃ + ....                 ...(7)

Equation (7) may be stated as follows :

The power of a combination of lenses in contact is the algebraic sum of the powers of individual lenses.

The combination of lenses is generally used in the design of objectives of microscopes, cameras, telescopes and other optical instruments.