Problem Solving: Obstacles to Problem Solving

Obstacles to Problem Solving

Broad strategies like means-end analysis, or a reliance on subroutines, help us to solve many problems. The fact remains, though, that some problems—whether an infuriat-ing crossword puzzle or a demoralizing job dispute—seem downright intractable. Why is this? And above all, what can we do to help people solve the problems they encounter?

Problem solvers inevitably bring certain assumptions and habits with them when-ever they approach a problem, and many of these assumptions are sensible and produc-tive. For instance, a taxi driver—even a beginner—doesn’t waste time wondering whether a magic carpet might be the fastest transport to the airport, and even a novice cook realizes that pickles are an unpalatable topping for the morning’s pancakes. Likewise (and more plausibly), in solving the anagram subufoal, you relied on the back-ground knowledge that some letter combinations are extremely rare in English, and so you didn’t waste time searching memory for a solution to this anagram that began with the letters bfl– or uua–; that helped you to narrow the options enormously and arrive more quickly at the actual solution.

The same sorts of assumptions, however, can sometimes lead us astray—if, for example, the assumptions are simply wrong or just inappropriate to the present situ-ation. In that case, the would-be problem solver can end up misled by a powerful mental set—the specific perspective that the person takes (including the assump-tions the person makes) in approaching the problem.

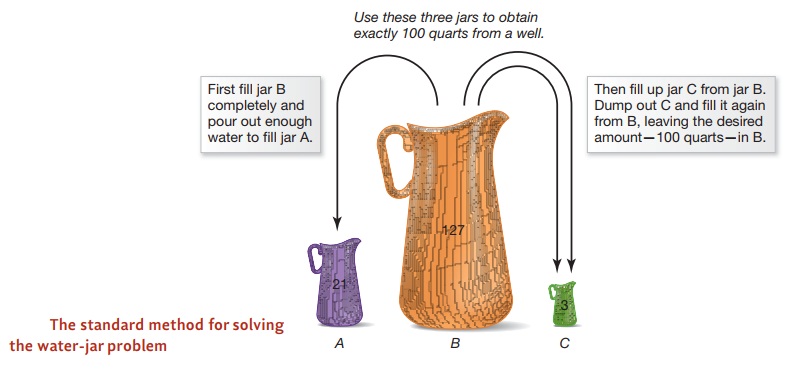
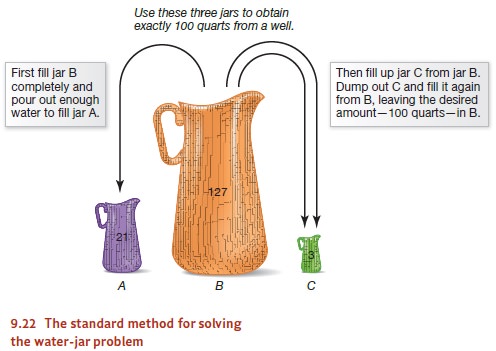
A classic study illustrates this point and shows how people can become fixated on one approach to a task. Participants were told that they had three jars, A, B, and C. Jar A held exactly 21 quarts; jar B held exactly 127 quarts; jar C held exactly 3 quarts. The participants’ job was to use these three jars to obtain exactly 100 quarts from a well.

Participants required a few minutes to solve this problem, but they generally did solve it. The solution is to fill B (127 quarts) completely and then pour out enough water from B to fill A. Now 106 quarts remain in B (127 – 21). Next, pour enough water out of B to fill up C (3 quarts), leaving 103 quarts in B. Finally, dump out C and fill it again from B, leaving the desired amount—100 quarts—in B (Figure 9.22).

Participants then did several more problems, all of the same type. The numerical val-ues differed in each problem, but in each case the solution could be obtained by the same sequence of steps: Fill B, pour from it into A, then pour from B into C, empty out C, and pour again from B into C. In each case, in other words, the desired amount could be reached by the arithmetical sequence of B – A – 2C.

After five such problems, the participants were given two critical tests. The first was a problem that required them to obtain 20 quarts, given jars whose volumes were 23, 49, and 3 quarts. The participants cheerfully solved this problem using the same sequence: 49 – 23 – (2 # 3). Most of them failed to notice a simpler method that requires only a single step (just B – C).

The participants were next asked to obtain 25 quarts, given jars of 28, 76, and 3 quarts. Note that here the only method that works is the direct one; that is, 28 – 3 - 25. But the mental set was so powerful that many subjects failed to solve the prob-lem altogether. They tried the old procedure, but it didn’t lead them to the goal (76 – 28 – [2 # 3] % 25), and they couldn’t find the alternative path! The mental set had made them so rigid that they became mentally blind (Luchins, 1942; for related examples, see Figure 9.19B and C).

Let’s be clear that the participants in this study weren’t being foolish. Once they found a way to solve a problem, it’s entirely sensible that they did not go looking for an alternate path. As an analogy, if you know how to scramble an egg, isn’t it reasonable to use the same tried-and-true technique each time rather than complicating your life by seeking a new procedure for each breakfast? The worry, though, is that this pattern— sensible as it generally is—can cause difficulties like those in the water-jar problem, often slowing (and sometimes even preventing) successful problem solving. (For more recent research on mental set, see, for example, Bilalic, 2008; Chrysikou & Weisberg, 2005; German & Barrett, 2005.)