Judgment: Thinking Dual-Process Theories

Dual-Process Theories

The two shortcuts we’ve discussed—availability and representativeness—generally work well. Things that are common in the world are likely also to be common in our memory, and so readily available for us; availability in memory is therefore often a good indicator of frequency in the world. Likewise, many of the categories we encounter are relatively homo-geneous; a reliance on representativeness, then, often leads us to the correct conclusions.

At the same time, these shortcuts can (and sometimes do) lead to errors. What’s worse, we can easily document the errors in consequential domains—medical profes-sionals drawing conclusions about someone’s health, politicians making judgments about international relations, business leaders making judgments about large sums of money. This demands that we ask: Is the use of the shortcuts inevitable? Are we simply stuck with this risk of error in human judgment?

The answer to these questions is plainly no, because people often rise above these shortcuts and rely on other, more laborious—but often more accurate—judgment strategies. For example, how many U.S. presidents have been Jewish? Here, you’re unlikely to draw on the availability heuristic (trying to think of relevant cases and bas-ing your answer on how easily these cases come to mind). Instead you’ll swiftly answer, “zero”—based probably on a bit of reasoning. (Your reasoning might be: “If there had been a Jewish president, this would have been notable and often discussed, and so I’d probably remember it. I don’t remember it. Therefore . . .”)

Likewise, we don’t always use the representativeness heuristic—and so we’re often not persuaded by a man-who story. Imagine, for example, that a friend says, “What doyou mean there’s no system for winning the lottery? I know a man who tried out his sys-tem last week, and he won!” Surely you’d respond by saying this guy just got lucky— relying on your knowledge about games of chance to overrule the evidence seemingly provided by this single case.

Examples like these (and more formal demonstrations of the same points—e.g., Nisbett et al., 1983) make it clear that sometimes we rely on judgment heuristics and sometimes we don’t. Apparently, therefore, we need a dual-process theory of judgment— one that describes two different types of thinking. The heuristics are, of course, one type of thinking; they allow us to make fast, efficient judgments in a wide range of circum-stances. The other type of thinking is usually slower and takes more effort—but it’s also less risky and often avoids the errors encouraged by heuristic use. A number of different terms have been proposed for these two types of thinking—intuition versus reasoning (Kahneman, 2003; Kahneman & Tversky, 1996); association-driven thought versus rule-driven thought (Sloman, 1996); a peripheral route to conclusions versus a central route (Petty & Cacioppo, 1985); intuition versus deliberation (Kuo et al., 2009), and so on. Each of these terms carries its own suggestion about how these two types of thought should be conceptualized, and theorists still disagree about this conceptualization. Therefore, many prefer the more neutral (but less transparent!) terms proposed by Stanovich and West (2000), who use System 1 as the label for the fast, automatic type of thinking and System2 as the label for the slower, more effortful type (Figure 9.9).

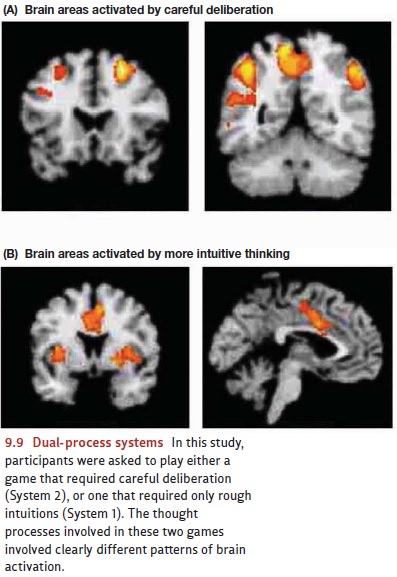
We might hope that people use System 1 for unimportant judg-ments and shift to System 2 when the stakes are higher. This would be a desirable state of affairs; but it doesn’t seem to be the case because, as we’ve mentioned, it’s easy to find situations in which people rely on System 1’s shortcuts even when making con-sequential judgments.

What does govern the choice between these two types of thinking? The answer has several parts. First, people are—not surprisingly—more likely to rely on the fast and easy strategies of System 1 if they ’re tired or pressed for time (e.g., Finucane, Alhakami, Slovic , & Johnson, 2000; D. Gilbert , 1989; Stanovich & West, 1998). Second, they ’re much more likely to use System 2’s better quality of thinking if the problem con-tains certain “triggers.” For example, people are more likely to rely on System 1 if asked to think about probabilities (“If you have this surgery, there’s a .2 chance of side effects”), but they ’re more likely to rely on System 2 when thinking about frequencies (“Two out of 10 people who have this surgery expe-rience side effects”). There’s some controversy about why this shift in data format has this effect, but it’s clear that we can improve human judgment simply by presenting the facts in the “right way ”—that is, in a format more likely to prompt System 2 thinking (Gigerenzer & Hoffrage, 1995, 1999; C. Lewis & Keren, 1999; Mellers et al., 2001; Mellers & McGraw, 1999).

The use of System 2 also depends on the type of evidence being considered. If, for example, the evidence is easily quantified in some way, this encourages System 2 thinking and makes errors less likely. As one illustration, people tend to be relatively sophisticated in how they think about sporting events. In such cases, each player’s performance is easily assessed via the game’s score or a race’s outcome, and each contest is immediately understood as a “sample” that may or may not be a good indicator of a player’s (or team’s) overall quality. In contrast, people are less sophisticated in how they think about a job candidate’s performance in an interview. Here it’s less obvious how to evaluate the candidate’s performance: How should we measure the candidate’s friendli-ness, or her motivation? People also seem not to realize that the 10 minutes of interview can be thought of as just a “sample” of evidence, and that other impressions might come from other samples (e.g., reinterviewing the person on a different day or seeing the person in a different setting; after J. Holland, Holyoak, Nisbett, & Thagard, 1986; Kunda & Nisbett, 1986).

Finally, some forms of education make System 2 thinking more likely. For example, training in the elementary principles of statistics seems to make students more alert to the problems of drawing a conclusion from a small sample and also more alert to the possibility of bias within a sample. This is, of course, a powerful argument for educa-tional programs that will ensure some basic numeracy—that is, competence in think-ing about numbers. But it’s not just courses in mathematics that are useful, because the benefits of training can also be derived from courses—such as those in psychology— that provide numerous examples of how sample size and sample bias affect any attempt to draw conclusions from evidence (Fong & Nisbett, 1991; Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz, & Woloshin, 2007; Lehman, Lempert, & Nisbett, 1988; Lehman & Nisbett, 1990; also see Perkins & Grotzer, 1997).

In short, then, our theorizing about judgment will need several parts. We rely on System 1 shortcuts, and these often serve us well—but can lead to error. We also can rise above the shortcuts and use System 2 thinking instead, and multiple factors govern whether (and when) this happens. Even so, the overall pattern of evidence points toward a relatively optimistic view—that our judgment is often accurate, and that it’s possible to make it more so.