Overview of Spectroscopy

Overview of Spectroscopy

The focus of this is photon spectroscopy, using ultraviolet, visible, and in- frared radiation. Because these techniques use a common set of optical devices for dispersing and focusing the radiation, they often are identified as optical spectros- copies. For convenience we will usually use the simpler term “spectroscopy” in place of photon spectroscopy or optical spectroscopy; however, it should be under- stood that we are considering only a limited part of a much broader area of analyti- cal methods. Before we examine specific spectroscopic methods, however, we first review the properties of electromagnetic radiation.

What Is Electromagnetic Radiation

Electromagnetic radiation, or light, is a form of energy whose behavior is described by the properties of both waves and particles. The optical properties of electromag- netic radiation, such as diffraction, are explained best by describing light as a wave. Many of the interactions between electromagnetic radiation and matter, such as ab- sorption and emission, however, are better described by treating light as a particle, or photon. The exact nature of electromagnetic radiation remains unclear, as it has since the development of quantum mechanics in the first quarter of the twentieth century.3 Nevertheless, the dual models of wave and particle behavior provide a use- ful description for electromagnetic radiation.

Wave Properties of Electromagnetic Radiation 

Electromagnetic radiation consists of oscillating electric and magnetic fields that propagate through space along a lin- ear path and with a constant velocity (Figure 10.1). In a vacuum, electromagnetic radiation travels at the speed of light, c, which is 2.99792 x 108 m/s. Electromagnetic radiation moves through a medium other than a vacuum with a velocity, v, less than that of the speed of light in a vacuum. The difference between v and c is small enough (< 0.1%) that the speed of light to three significant figures, 3.00 x 108 m/s, is sufficiently accurate for most purposes.

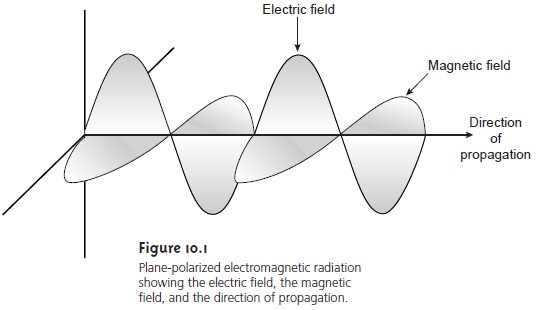
Oscillations in the electric and magnetic fields are perpendicular to each other, and to the direction of the wave’s propagation. Figure 10.1 shows an example of plane-polarized electromagnetic radiation consisting of an oscillating electric field and an oscillating magnetic field, each of which is constrained to a single plane. Normally, electromagnetic radiation is unpolarized, with oscillating electric and magnetic fields in all possible planes oriented perpendicular to the direction of propagation.

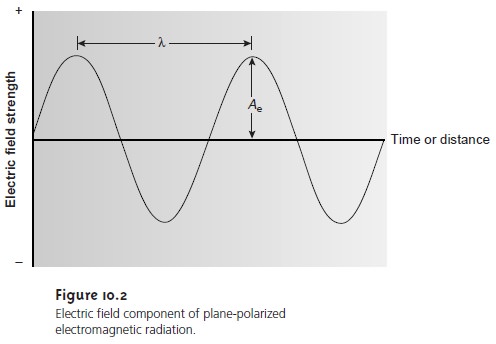
The interaction of electromagnetic radiation with matter can be explained using either the electric field or the magnetic field. For this reason, only the electric field component is shown in Figure 10.2. The oscillating electric field is described by a sine wave of the form

E = A_e sin(2πvt + Φ)

where E is the magnitude of the electric field at time t, A_e is the electric field’s maxi- mum amplitude, v is the frequency, or the number of oscillations in the electric field per unit time, and Φ is a phase angle accounting for the fact that the electric field’s magnitude need not be zero at t = 0. An identical equation can be written for the magnetic field, M

M = A_m sin(2vt + Φ)

where A_m is the magnetic field’s maximum amplitude.

An electromagnetic wave, therefore, is characterized by several fundamental properties, including its velocity, amplitude, frequency, phase angle, polarization, and direction of propagation. Other properties, which are based on these funda- mental properties, also are useful for characterizing the wave behavior of electro- magnetic radiation. The wavelength of an electromagnetic wave, λ, is defined as the distance between successive maxima, or successive minima (see Figure 10.2). For ultraviolet and visible electromagnetic radiation the wavelength is usually expressed in nanometers (nm, 10–9 m), and the wavelength for infrared radiation is given in microns (μm, 10–6 m). Unlike frequency, wavelength depends on the electromag- netic wave’s velocity, where

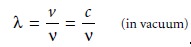
Thus, for electromagnetic radiation of frequency, v, the wavelength in vacuum is longer than in other media. Another unit used to describe the wave properties of electromagnetic radiation is the wavenumber, –v, which is the reciprocal of wave-

length

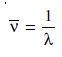
Wavenumbers are frequently used to characterize infrared radiation, with the units given in reciprocal centimeter (cm–1).

Two additional wave properties are power, P, and intensity, I, which give the flux of energy from a source of electromagnetic radiation.

Particle Properties of Electromagnetic Radiation 

When a sample absorbs electro- magnetic radiation it undergoes a change in energy. The interaction between the sample and the electromagnetic radiation is easiest to understand if we assume that electromagnetic radiation consists of a beam of energetic particles called photons. When a photon is absorbed by a sample, it is “destroyed,” and its energy acquired by the sample.5 The energy of a photon, in joules, is related to its frequency, wave- length, or wavenumber by the following equations

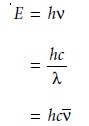
where h is Planck’s constant, which has a value of 6.626 x 10–34 J 1 s.

The energy of a photon provides an additional characteristic property of electro- magnetic radiation.

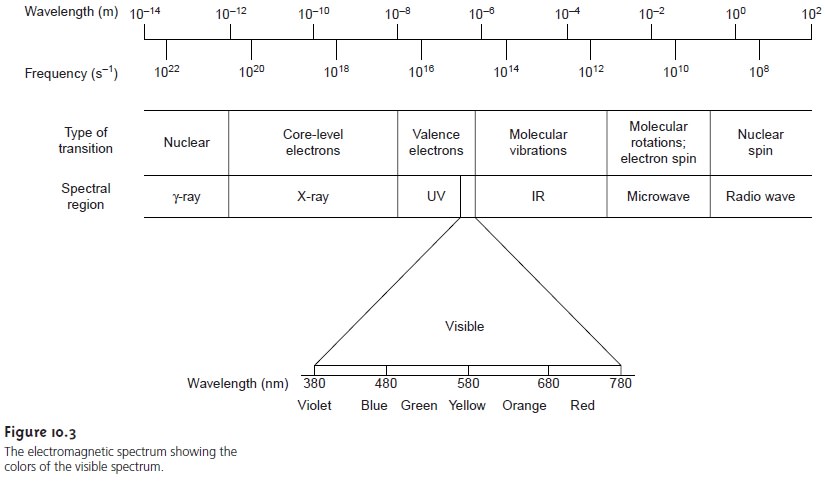
The Electromagnetic Spectrum 

The frequency and wavelength of electromagnetic radiation vary over many orders of magnitude. For convenience, electromagnetic radiation is divided into different regions based on the type of atomic or molecular transition that gives rise to the absorption or emission of photons (Figure 10.3). The boundaries describing the electromagnetic spectrum are not rigid, and an overlap between spectral regions is possible.

Measuring Photons as a Signal

In the previous section we defined several characteristic properties of electromag- netic radiation, including its energy, velocity, amplitude, frequency, phase angle, polarization, and direction of propagation. Spectroscopy is possible only if the pho- ton’s interaction with the sample leads to a change in one or more of these charac- teristic properties.

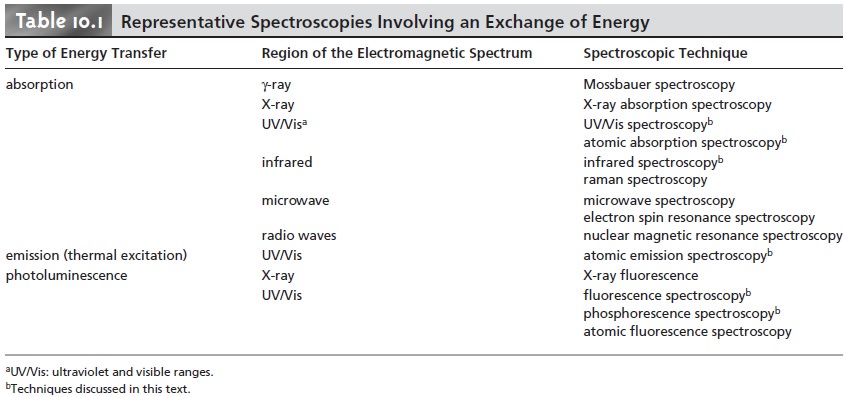
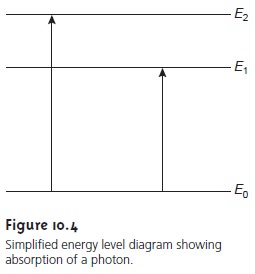
Spectroscopy is conveniently divided into two broad classes. In one class of techniques, energy is transferred between a photon of electromagnetic radiation and the analyte (Table 10.1). In absorption spectroscopy the energy carried by a photon is absorbed by the analyte, promoting the analyte from a lower-energy state to a higher-energy, or excited, state (Figure 10.4). The source of the energetic state de- pends on the photon’s energy. The electromagnetic spectrum in Figure 10.3, for ex- ample, shows that absorbing a photon of visible light causes a valence electron in the analyte to move to a higher-energy level. When an analyte absorbs infrared radi- ation, on the other hand, one of its chemical bonds experiences a change in vibra- tional energy.

The intensity of photons passing through a sample containing the analyte is at- tenuated because of absorption. The measurement of this attenuation, which we call absorbance, serves as our signal. Note that the energy levels in Figure 10.4 have well-defined values (i.e., they are quantized). Absorption only occurs when the pho- ton’s energy matches the difference in energy, ∆E, between two energy levels. 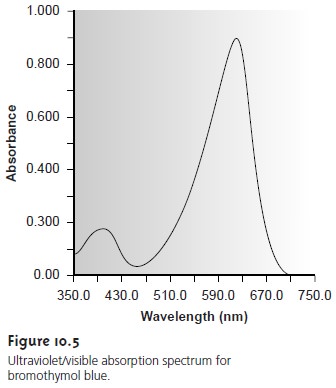A plot of absorbance as a function of the photon’s energy is called an absorbance spec- trum (Figure 10.5).

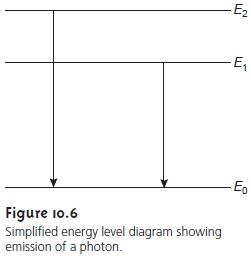
Emission of a photon occurs when an analyte in a higher-energy state returns to a lower-energy state (Figure 10.6). The higher-energy state can be achieved in several ways, including thermal energy, radiant energy from a photon, or by a chemical reaction. 

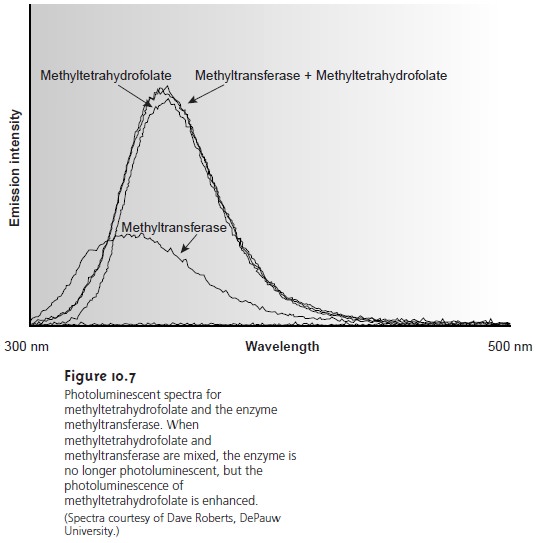
Emission following the absorption of a photon is also called photoluminescence, and that following a chemical reaction is called chemilumi- nescence. A typical emission spectrum is shown in Figure 10.7.

In the second broad class of spectroscopy, the electromagnetic radiation under- goes a change in amplitude, phase angle, polarization, or direction of propagation as a result of its refraction, reflection, scattering, diffraction, or dispersion by the sample. Several representative spectroscopic techniques are listed in Table 10.2.