Magnetic induction at a point along the equatorial line of a bar magnet

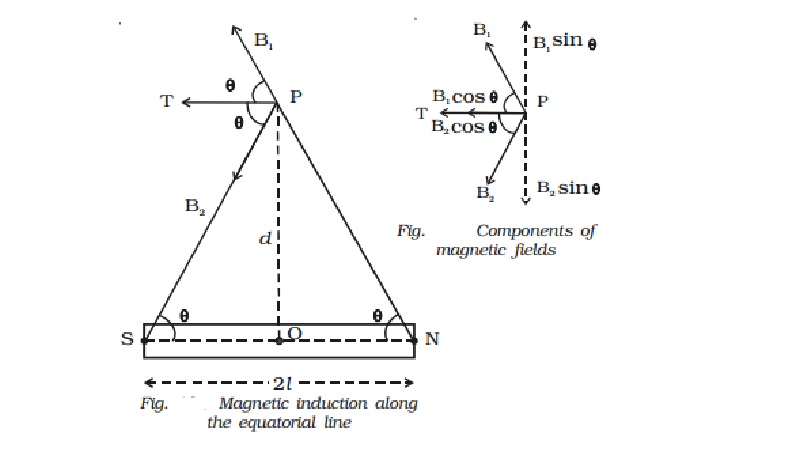
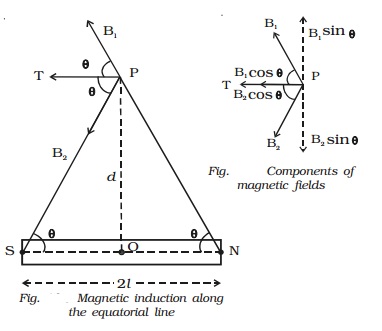
Magnetic induction at a point along the equatorial line of a bar magnet

NS is the bar magnet of length 2l and pole strength m. P is a point on the equatorial line at a distance d from its mid point O (Fig.).

Magnetic induction (B₁) at P due to north pole of the magnet,

B₁ = ?₀/4π  .  m/NP² along NP

= ?₀/4π  .  m/(d²+l²) along NP

NP² = NO² + OP²

Magnetic induction (B₂) at P due to south pole of the magnet,

B₂ = ?₀/4π  .  m/PS² along PS

= ?₀/4π  .  m/(d²+l²) along PS

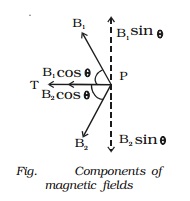
Resolving B1 and B2 into their horizontal and vertical components.

Vertical components B1 sin θ and B2 sin θ are equal and opposite and therefore cancel each other (Fig.).

The horizontal components B1 cos θ and B2 cos θ will get added along PT.

Resultant magnetic induction at P due to the bar magnet is

B = B₁ cos θ + B₂ cos θ. (along PT)

After apply B₁ and B₂

B = = ?₀/4π  .  M/d³

The direction of ?B? is along PT parallel to NS.

Coulomb?s inverse square law

Coulomb?s inverse square law states that the force of attraction or repulsion between the two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them.