Chapter: Modern Analytical Chemistry: Spectroscopic Methods of Analysis
Limitations to Beer’s Law
Limitations to Beer’s Law
According to Beer’s
law, a calibration curve of absorbance versus
the concentration of analyte
in a series of standard solutions should be a straight line with an intercept
of 0 and a slope
of ab or εb. In
many cases, however,
calibration curves are found to be
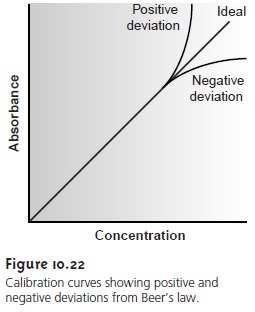
nonlinear (Figure 10.22).
Deviations from linearity are divided into
three cate- gories: fundamental, chemical, and instrumental.
Fundamental Limitations to Beers Law
Beer’s law is a limiting
law that is valid
only for low concentrations of analyte. There
are two contributions to this funda- mental limitation to Beer’s law. At higher concentrations the individual particles
of analyte no longer behave independently of one another. The resulting
interaction between particles of analyte may change the value of ε. A second contribution is that the absorptivity, a, and molar absorptivity, ε, depend on the sample’s
refractive index. Since the refractive index varies with the analyte’s
concentration, the values of
a
and ε will change. For sufficiently low concentrations of analyte, the refractive
index remains essentially constant, and the calibration curve is linear.
Chemical Limitations to Beer’s Law
Chemical
deviations from Beer’s law can occur when the absorbing
species is involved
in an equilibrium reaction. Consider, as an example, an analysis for the weak acid, HA. To construct
a Beer’s law calibra-
tion curve, several standards containing known total concentrations of HA, Ctot, are prepared and the absorbance of each is measured at the same wavelength. Since
HA is a weak acid, it exists in equilibrium with its conjugate weak base, A–
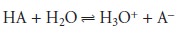
If both HA and A– absorb at the selected wavelength, then Beers
law is written as
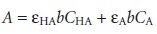 10.7
10.7
where CHA and CA are the equilibrium concentrations of HA and A–.
Since the weak acid’s total concentration, Ctot, is
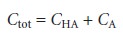
the concentrations of HA and A– can be written as
CHA = αHACtot
…… 10.8
CA =
(1– αHA)Ctot …… 10.9
where αHA is the fraction
of weak acid present as HA. Substituting equations 10.8 and 10.9 into equation
10.7, and rearranging, gives
A =
(εHAαHA + εA – εAαHA)bCtot
…… 10.10
Because values of αHA may depend on the concentration of HA, equation
10.10 may not be linear. A Beer’s law
calibration curve of A versus Ctot will
be linear if one of two
conditions is met. If the wavelength is chosen such that εHA and εA are equal,
then equation 10.10 simplifies to
A = εAbCtot
and a linear Beer’s law calibration curve is realized.
Alternatively, if αHA is held con- stant for all standards, then equation 10.10
will be a straight line at all wavelengths.
Because HA is a weak
acid, values of αHA change
with pH. To maintain a constant
value for αHA, therefore, we need to buffer each standard solution
to the same pH. Depending on the relative values of εHA and εA, the
calibration curve will
show a positive or negative deviation from Beer’s law
if the standards are not buffered to the same pH.
Instrumental Limitations to Beer’s Law
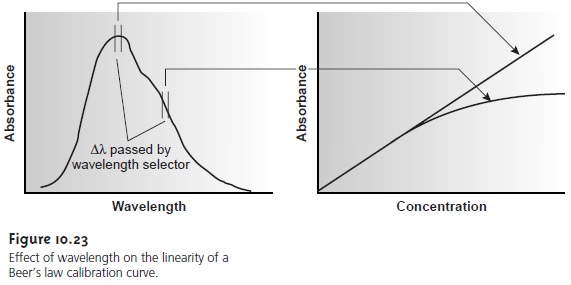
There are two principal instrumental limi- tations to Beer’s law. The first limitation is that Beer’s law is strictly valid for purely monochromatic radiation; that is, for radiation consisting of only one wavelength.
As we learned, however, even the best wavelength selector
passes radiation with a small, but finite effective bandwidth. Using
polychromatic radia- tion always gives a negative
deviation from Beer’s law, but is minimized
if the value of ε is essentially constant
over the wavelength range passed by the wavelength se- lector. For this
reason, as shown
in Figure 10.23,
it is preferable to make
absorbance measurements at a broad absorption peak. In addition, deviations from Beer’s
law are less serious
if the effective bandwidth from the source
is less than one tenth
of the natural bandwidth of the absorbing species. When
measurements must be made on a slope, linearity is improved by using a narrower effective bandwidth.
Stray radiation is the second contribution to instrumental deviations from Beer’s law. Stray radiation arises from imperfections within the wavelength selector that allows extraneous light to “leak” into the instrument. Stray radiation adds an additional contribution, Pstray, to the radiant power reaching the detector; thus
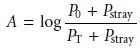
For small concentrations of analyte, Pstray is significantly smaller
than P0 and PT, and the
absorbance is unaffected by the stray
radiation. At higher
concentrations of ana- lyte, however, Pstray is no longer
significantly smaller than PT and the absorbance is smaller than expected. The result is a negative
deviation from Beer’s
law.
Related Topics