Chapter: 11th Physics : UNIT 6 : Gravitation
Kepler’s Third Law and The Astronomical Distance
Kepler’s Third Law and The Astronomical Distance
When Kepler derived his three laws, he strongly relied on Tycho Brahe’s astronomical observation. In his third law, he formulated the relation between the distance of a planet from the Sun to the time period of revolution of the planet. Astronomers cleverly used geometry and trigonometry to calculate the distance of a planet from the Sun in terms of the distance between Earth and Sun. Here we can see how the distance of Mercury and Venus from the Sun were measured. The Venus and Mercury, being inner planets with respect to Earth, the maximum angular distance they can subtend at a point on Earth with respect to the Sun is 46 degree for Venus and 22.5 degree for Mercury. It is shown in the Figure 6.28
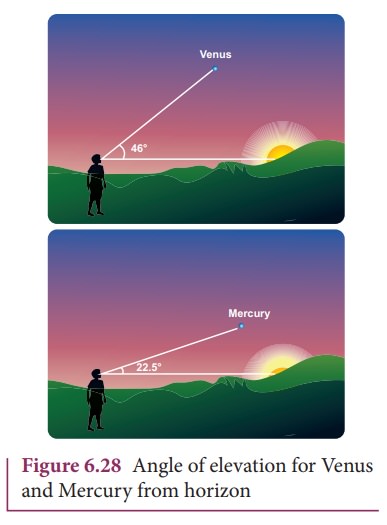
Figure 6.29 shows that when Venus is at maximum elongation (i.e., 46 degree) with respect to Earth, Venus makes 90 degree to Sun. This allows us to find the distance between Venus and Sun. The distance between Earth and Sun is taken as one Astronomical unit (1 AU).
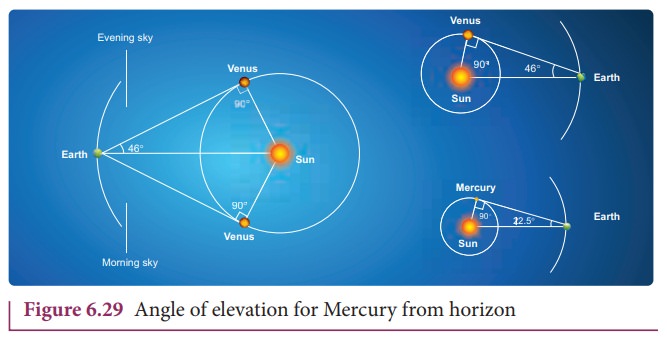
The trigonometric relation satisfied by this right angled triangle is shown in Figure 6.29.

Here sin 46̊ = 0.77. Hence Venus is at a distance of 0.77 AU from Sun. Similarly, the distance between Mercury (θ is 22.5 degree) and Sun is calculated as 0.38 AU. To find the distance of exterior planets like Mars and Jupiter, a slightly different method is used. The distances of planets from the Sun is given in the table below.
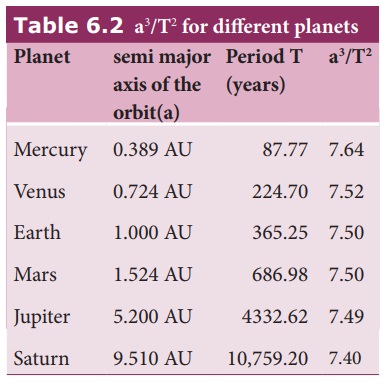
It is to be noted that to verify the Kepler’s law we need only high school level geometry and trigonometry.
Related Topics