Explanation of Nuclear binding energy curve

Nuclear Binding energy

When the protons and neutrons combine to form a nucleus, the mass that disappears (mass defect, ∆m) is converted into an equivalent amount of energy (∆mc²). This energy is called the binding energy of the nucleus.

      Binding energy = [Zm_P + Nm_n - m] c²

=  ∆m c²

The binding energy of a nucleus determines its stability against disintegration. In other words, if the binding energy is large, the nucleus is stable and vice versa.

The binding energy per nucleon is

BE/ A = Binding energy of the nucleus  / Total number of nucleons

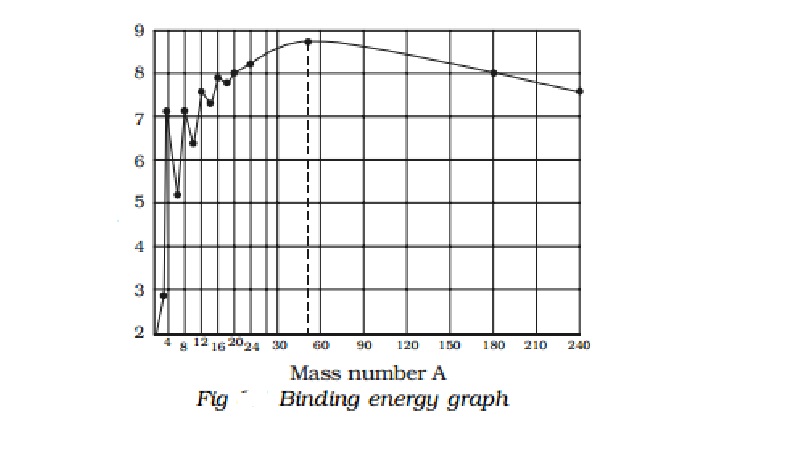
It is found that the binding energy per nucleon varies from element to element. A graph is plotted with the mass number A of the nucleus along the X−axis and binding energy per nucleon along the Y-axis (Fig).

Explanation of binding energy curve

       i.            The binding energy per nucleon increases sharply with mass number A upto 20. It increases slowly after A = 20. For A<20, there exists recurrence of peaks corresponding to those nuclei, whose mass numbers are multiples of four and they contain not only equal but also even number of protons and neutrons. Example: ₂He⁴, ₄Be⁸, ₆C¹², ₈O¹⁶, and ₁₀Ne²⁰. The curve becomes almost flat for mass number between 40 and 120. Beyond 120, it decreases slowly as A increases.

     ii.            The  binding  energy  per  nucleon  reaches  a  maximum  of MeV at A=56, corresponding to the iron nucleus (₂₆Fe⁵⁶). Hence, iron nucleus is the most stable.

  iii.            The average binding energy per nucleon is about 8.5 MeV for nuclei having mass number ranging between 40 and 120. These elements are comparatively more stable and non radioactive.

  iv.            For higher mass numbers the curve drops slowly and the BE/A is about 7.6 MeV for uranium. Hence, they are unstable and radioactive.

     v.            The lesser amount of binding energy for lighter and heavier nuclei explains nuclear fusion and fission respectively. A large amount of energy will be liberated if lighter nuclei are fused to form heavier one (fusion) or if heavier nuclei are split into lighter ones (fission).