Classification of nuclei and Properties of nucleus Nuclear size

The atomic nucleus was discovered by Earnest Rutherford in 1911. Rutherford's experiment on scattering of alpha particles proved that the mass of the atom and the positive charge is concentrated in a very small central core called nucleus. The dimension of nucleus is much smaller than the overall dimension of the atom. The nucleus is surrounded by orbiting electrons.

Nucleus

The nucleus consists of the elementary particles, protons and neutrons which are known as nucleons. A proton has positive charge of the same magnitude as that of electron and its rest mass is about 1836 times the mass of an electron. A neutron is electrically neutral, whose mass is almost equal to the mass of the proton. The nucleons inside the nucleus are held together by strong attractive forces called nuclear forces.

A nucleus of an element is represented as _ZX^A, where X is the chemical symbol of the element. Z represents the atomic number which is equal to the number of protons and A, the mass number which is equal to the total number of protons and neutrons. The number of neutrons is represented as N which is equal to A−Z. For example, the chlorine nucleus is represented as ₁₇Cl³⁵. It contains 17 protons and 18 neutrons.

1Classification of nuclei

(i) Isotopes

Isotopes are atoms of the same element having the same atomic number Z but different mass number A. The nuclei ₁H ¹, ₁H² and ₁H³ are the isotopes of hydrogen. In other words isotopes of an element contain the same number of protons but different number of neutrons. As the atoms of isotopes have identical electronic structure, they have identical chemical properties and placed in the same location in the periodic table.

(ii) Isobars

Isobars are atoms of different elements having the same mass number A, but different atomic number Z. The nuclei ₈O¹⁶ and ₇N¹⁶ represent two isobars. Since isobars are atoms of different elements, they have different physical and chemical properties.

(iii) Isotones

Isotones are atoms of different elements having the same number of neutrons. ₆C¹⁴ and ₈O¹⁶ are some examples of isotones.

2.General properties of nucleus Nuclear size

According to Rutherford's á−particle scattering experiment, the distance of the closest approach of á − particle to the nucleus was taken as a measure of nuclear radius, which is approximately 10⁻¹⁵m. If the nucleus is assumed to be spherical, an empirical relation is found to hold good between the radius of the nucleus R and its mass number A. It is given by

R ∝∝ A^1/3

R = r_oA^1/3

where r_o is the constant of proportionality and is equal to 1.3 F (1 Fermi, F = 10⁻¹⁵ m)

Nuclear density

The nuclear density ñ_N can be calculated from the mass and size of the nucleus.

ρ_N = Nuclear mass / Nuclear volume

Nuclear mass = Am_N

where, A = mass number

and m_N = mass of one nucleon and is approximately equal to 1.67 × 10⁻²⁷ kg

Nuclear volume = 4/3 πR³

ρ_N = m_N / ( 4/3 πr₀³)

Substituting the known values, the nuclear density is calculated as 1.816 × 10¹⁷ kg m⁻³ which is almost a constant for all the nuclei irrespective of its size.

The high value of the nuclear density shows that the nuclear matter is in an extremely compressed state.

Nuclear charge

The charge of a nucleus is due to the protons present in it. Each proton has a positive charge equal to 1.6 × 10⁻¹⁹ C.

       The nuclear charge = Ze, where Z is the atomic number.

Atomic mass unit

It is convenient to express the mass of a nucleus in atomic mass unit (amu), though the unit of mass is kg. One atomic mass unit is considered as one twelfth of the mass of carbon atom ₆C ¹². Carbon of atomic number 6 and mass number 12 has mass equal to 12 amu.

1 amu = 1.66 × 10⁻²⁷ kg

The mass of a proton, m_p = 1.007276 amu

This is equal to the difference in mass of the hydrogen atom which is 1.007825 amu and the mass of electron.

The mass of a neutron, m_n = 1.008665 amu

The energy equivalence of one amu can be calculated in electron-volt

Einstein's mass energy relation is, E = mc² Here, m = 1 amu = 1.66 × 10⁻²⁷ kg

c = 3 × 10⁸ ms⁻¹

E = 1.66 × 10⁻²⁷ × (3 × 10⁸)² J

One electron-volt (eV) is defined as the energy of an electron when it is accelerated through a potential difference of 1 volt.

1 eV = 1.6 × 10⁻¹⁹ coulomb × 1 volt 1 eV = 1.6 × 10⁻¹⁹ joule

Hence, E = 1.66 × 10 ^{− 27} × (3 ×10 ⁸ )² / 1.6 ×10^{-19 eV}

^{= = 931 million electronvolt = 931 MeV}

Thus, energy equivalent of 1 amu = 931 MeV

Nuclear mass

As the nucleus contains protons and neutrons, the mass of the nucleus is assumed to be the mass of its constituents.

Assumed nuclear mass = Zm_P + Nm_n,

where m_p and m_n are the mass of a proton and a neutron respectively. However, from the measurement of mass by mass spectrometers, it is found that the mass of a stable nucleus (m) is less than the total mass of the nucleons.

i.e    mass of a nucleus, m < (Zm_p + Nm_n) Zm_p + Nm_N - m = ∆m

where ∆m is the mass defect

Thus, the difference in the total mass of the nucleons and the actual mass of the nucleus is known as the mass defect.

Note : In any mass spectrometer, it is possible to determine only the mass of the atom, which includes the mass of Z electrons. If M represents the mass of the atom, then the mass defect can be written as

∆m  = Zm_P + Nm_n + Zm_e - M

= Zm_H + Nm_n - M

where m_H represents the mass of one hydrogen atom

Binding energy

When the protons and neutrons combine to form a nucleus, the mass that disappears (mass defect, ∆m) is converted into an equivalent amount of energy (∆mc²). This energy is called the binding energy of the nucleus.

      Binding energy = [Zm_P + Nm_n - m] c²

=  ∆m c²

The binding energy of a nucleus determines its stability against disintegration. In other words, if the binding energy is large, the nucleus is stable and vice versa.

The binding energy per nucleon is

BE/ A = Binding energy of the nucleus  / Total number of nucleons

It is found that the binding energy per nucleon varies from element to element. A graph is plotted with the mass number A of the nucleus along the X−axis and binding energy per nucleon along the Y-axis (Fig).

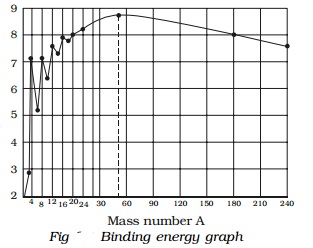
Explanation of binding energy curve

       i.            The binding energy per nucleon increases sharply with mass number A upto 20. It increases slowly after A = 20. For A<20, there exists recurrence of peaks corresponding to those nuclei, whose mass numbers are multiples of four and they contain not only equal but also even number of protons and neutrons. Example: ₂He⁴, ₄Be⁸, ₆C¹², ₈O¹⁶, and ₁₀Ne²⁰. The curve becomes almost flat for mass number between 40 and 120. Beyond 120, it decreases slowly as A increases.

     ii.            The  binding  energy  per  nucleon  reaches  a  maximum  of MeV at A=56, corresponding to the iron nucleus (₂₆Fe⁵⁶). Hence, iron nucleus is the most stable.

  iii.            The average binding energy per nucleon is about 8.5 MeV for nuclei having mass number ranging between 40 and 120. These elements are comparatively more stable and non radioactive.

  iv.            For higher mass numbers the curve drops slowly and the BE/A is about 7.6 MeV for uranium. Hence, they are unstable and radioactive.

     v.            The lesser amount of binding energy for lighter and heavier nuclei explains nuclear fusion and fission respectively. A large amount of energy will be liberated if lighter nuclei are fused to form heavier one (fusion) or if heavier nuclei are split into lighter ones (fission).