Conservation of angular momentum with Illustration

Conservation of angular momentum

The angular momentum of a rotating rigid body is, L = I ω

The torque acting on a rigid body is, τ = dL/dt

When no external torque acts on the system, τ =dL/ _dt  = 0

(i.e) L = I ω = constant

Total angular momentum of the body = constant

(i.e.) when no external torque acts on the body, the net angular momentum of a rotating rigid body remains constant. This is known as law of conservation of angular momentum.

Illustration of conservation of angular momentum

From the law of conservation of angular momentum, I ω = constant

(ie)  ω ∝ 1/l ∝ , the angular velocity of rotation is inversely proportional to the moment of inertia of the system.

Following are the examples for law of conservation of angular momentum.

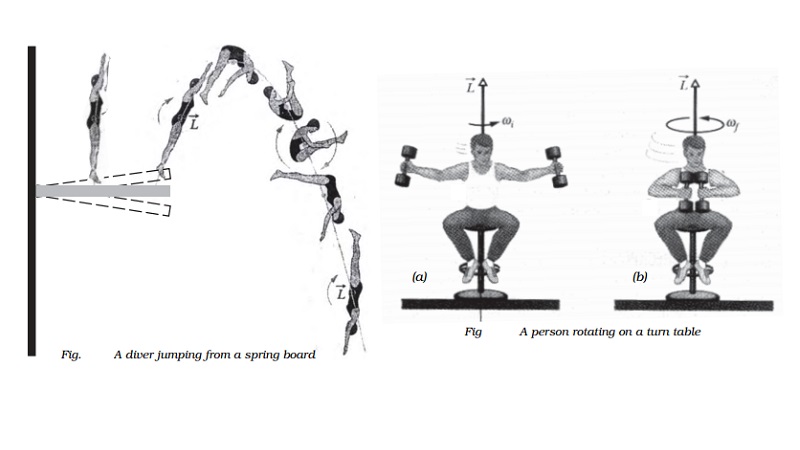
1. A diver jumping from springboard sometimes exhibits somersaults in air before reaching the water surface, because the diver curls his body to decrease the moment of inertia and increase angular velocity. When he is about to reach the water surface, he again outstretches his limbs. This again increases moment of inertia and decreases the angular velocity. Hence, the diver enters the water surface with a gentle speed.

2. A ballet dancer can increase her angular velocity by folding her arms, as this decreases the moment of inertia.

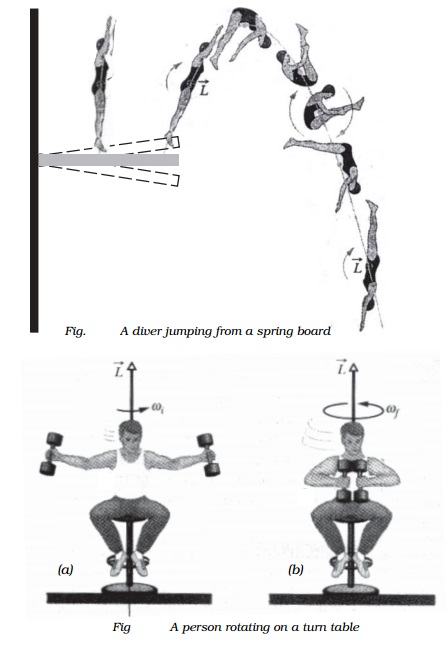
3. Fig. a shows a person sitting on a turntable holding a pair of heavy dumbbells one in each hand with arms outstretched. The table is rotating with a certain angular velocity. The person suddenly pushes the weight towards his chest as shown Fig. b, the speed of rotation is found to increase considerably.

4.The angular velocity of a planet in its orbit round the sun increases when it is nearer to the Sun, as the moment of inertia of the planet about the Sun decreases.