Relation between torque and angular acceleration

Relation between torque and angular acceleration

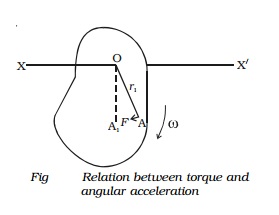
Let us consider a rigid body rotating about a fixed axis X0X′ with angular velocity ω (Fig.).

The force acting on a particle of mass m₁ situated at A, at a distance r₁, from the axis of rotation = mass ? acceleration

= m₁ ? d/dt(r₁ω)

 = (m₁ r₁)dω /dt

= (m₁ r₁)d²θ/dt²

The moment of this force about the axis of rotation

= Force ? perpendicular distance

= (m₁ r₁)d²θ/dt²   x r₁

Therefore, the total moment of all the forces acting on all the particles

or τ = Iα

where ∑ m₁r₁² = moment of inertia I of the rigid body and α = d² θ /dt² angular acceleration.

Relation between torque and angular momentum

The angular momentum of a rotating rigid body is, L = I ω

Differentiating the above equation with respect to time,

dL/dt = I(d ω /dt) = Ia

where α = dω/dt   angular acceleration of the body.

But torque τ = Iα

Therefore, torque τ = dL/dt

Thus the rate of change of angular momentum of a body is equal to the external torque acting upon the body.

Conservation of angular momentum

The angular momentum of a rotating rigid body is, L = I ω

The torque acting on a rigid body is, τ = dL/dt

When no external torque acts on the system, τ =dL/ _dt  = 0

(i.e) L = I ω = constant

Total angular momentum of the body = constant

(i.e.) when no external torque acts on the body, the net angular momentum of a rotating rigid body remains constant. This is known as law of conservation of angular momentum.