Simple harmonic motion

Oscillations

Any motion that repeats itself after regular intervals of time is known as a periodic motion. The examples of periodic motion are the motion of planets around the Sun, motion of hands of a clock, motion of the balance wheel of a watch, motion of Halley?s comet around the Sun observable on the Earth once in 76 years.

If a body moves back and forth repeatedly about a mean position, it is said to possess oscillatory motion. Vibrations of guitar strings, motion of a pendulum bob, vibrations of a tuning fork, oscillations of mass suspended from a spring, vibrations of diaphragm in telephones and speaker system and freely suspended springs are few examples of oscillatory motion. In all the above cases of vibrations of bodies, the path of vibration is always directed towards the mean or equilibrium position.

The oscillations can be expressed in terms of simple harmonic functions like sine or cosine function. A harmonic oscillation of constant amplitude and single frequency is called simple harmonic motion (SHM).

Simple harmonic motion

A particle is said to execute simple harmonic motion if its acceleration is directly proportional to the displacement from a fixed point and is always directed towards that point.

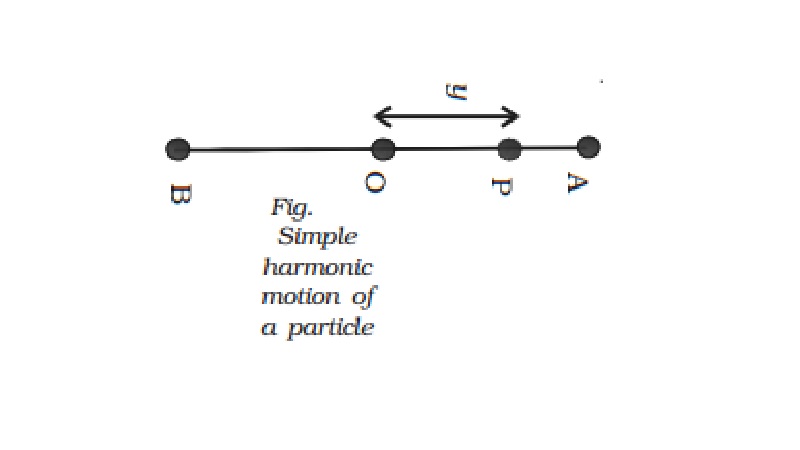
Consider a particle P executing SHM along a straight line between A and B about the mean position O (Fig.). The acceleration of the particle is always directed towards a fixed point on the line and its magnitude is proportional to the displacement of the particle from this point.

Consider a particle P executing SHM along a straight line between A and B about the mean position O (Fig.). The acceleration of the particle is always directed towards a fixed point on the line and its magnitude is proportional to the displacement of the particle from this point.

(i.e) a α y

By definition a = −ω² y

where ω is a constant known as angular frequency of the simple harmonic motion. The negative sign indicates that the acceleration is opposite to the direction of displacement. If m is the mass of the particle, restoring force that tends to bring back the particle to the mean position is given by

F = −m ω² y

or        F = −k y

The constant k = m ω², is called force constant or spring constant. Its unit is N m⁻¹. The restoring force is directed towards the mean position.

Thus, simple harmonic motion is defined as oscillatory motion about a fixed point in which the restoring force is always proportional to the displacement and directed always towards that fixed point.