Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Banking of curved roads and tracks and Condition for skidding
Banking of curved roads and tracks
When a car goes round a level curve, the force of friction between the tyres and the road provides the necessary centripetal force. If the frictional force, which acts as centripetal force and keeps the body moving along the circular road is not enough to provide the necessary centripetal force, the car will skid. In order to avoid skidding, while going round a curved path the outer edge of the road is raised above the level of the inner edge. This is known as banking of curved roads or tracks.
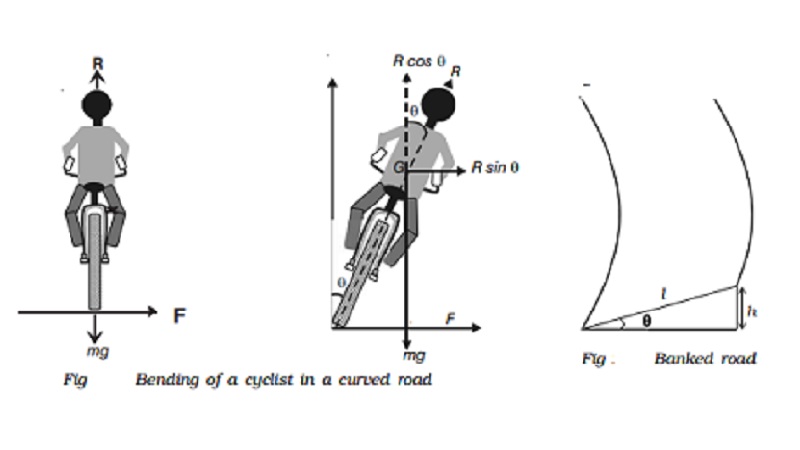
Bending of a cyclist round a curve
A cyclist has to bend slightly towards the centre of the circular track in order to take a safe turn without slipping.
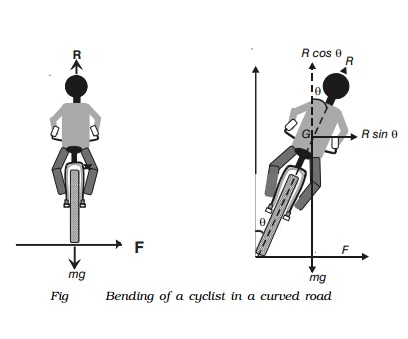
Fig. shows a cyclist taking a turn towards his right on a circular path of radius r. Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components: (i) the component R sin θ, acting towards the centre of the curve providing necessary centripetal force for circular motion and (ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
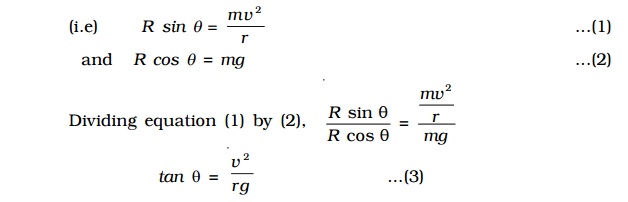
(i.e) R sin θ = mv2/r ...(1)
and R cos θ = mg ...(2)
Dividing equation (1) by (2),
Rsin θ/R cos θ = (mv2/r ) / mg
tan θ = v2/rg ...(3)
Thus for less bending of cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger.
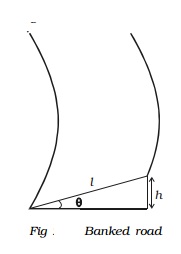
For a banked road (Fig.), let h be the elevation of the outer edge of the road above the inner edge and l be the width of the road then,
sin θ = h/l ...(4)
For small values of θ, sin θ = tan θ
Therefore from equations (3) and (4)
tan θ = h/l = v2/rg
Obviously, a road or track can be banked correctly only for a particular speed of the vehicle. Therefore, the driver must drive with a particular speed at the circular turn. If the speed is higher than the desired value, the vehicle tends to slip outward at the turn but then the frictional force acts inwards and provides the additional centripetal force. Similarly, if the speed of the vehicle is lower than the desired speed it tends to slip inward at the turn but now the frictional force acts outwards and reduces the centripetal force.
Condition for skidding
When the centripetal force is greater than the frictional force, skidding occurs. If ? is the coefficient of friction between the road and tyre, then the limiting friction (frictional force) is f = ?R where normal reaction R = mg
∴f = m (mg)
Thus for skidding,
Centripetal force > Frictional force
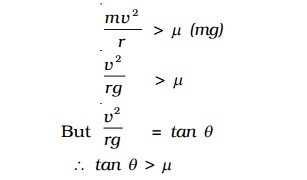
mv2/r > m (mg)
v2/rg >
But v2/rg=tan θ
∴ tan θ > m
(i.e) when the tangent of the angle of banking is greater than the coefficient of friction, skidding occurs.
Related Topics