Applications of centripetal forces

Applications of centripetal forces

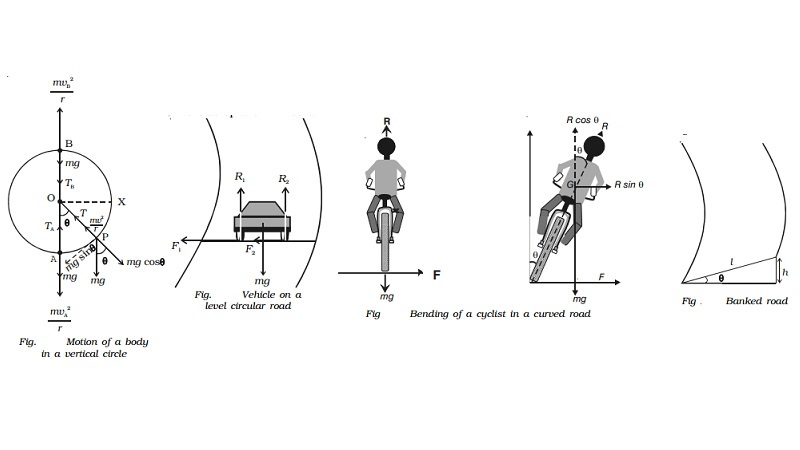
(i) Motion in a vertical circle

Let us consider a body of mass m tied to one end of the string which is fixed at O and it is moving in a vertical circle of radius r about the point O as shown in Fig. 2.41. The motion is circular but is not uniform, since the body speeds up while coming down and slows down while going up.

Suppose the body is at P at any instant of time t, the tension T in the string always acts towards 0.

The weight mg of the body at P is resolved along the string as mg cos Î¸ which acts outwards and mg sin Î¸, perpendicular to the string.

When the body is at P, the following forces acts on it along the string.

i.          mg cos Î¸ acts along OP (outwards)

ii.            tension T acts along PO (inwards)

Net force on the body at P acting along PO = T - mg cos Î¸

This must provide the necessary centripetal force mv/r2 .

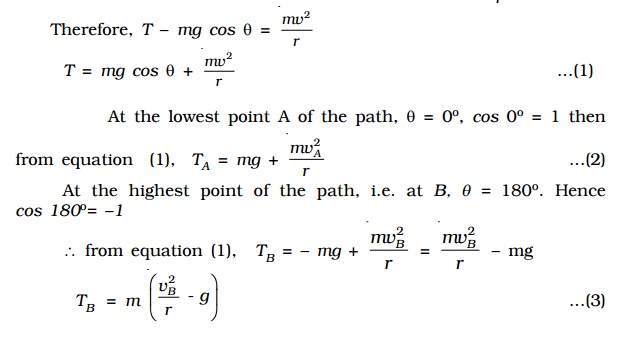
If T_B > 0, then the string remains taut while if T_B < 0, the string slackens and it becomes impossible to complete the motion in a vertical circle.

If the velocity v_B is decreased, the tension T_B in the string also decreases, and becomes zero at a certain minimum value of the speed called critical velocity. Let v_C be the minimum value of the velocity, then at v_B = v_c , TB = 0. Therefore from equation (3),

mv2C/r ? mg = 0  (or) v2C = rg

vc = root[rg]

If the velocity of the body at the highest point B is below this critical velocity, the string becomes slack and the body falls downwards instead of moving along the circular path. In order to ensure that the velocity v_B at the top is not lesser than the critical velocity Ã-[ rg ], the minimum velocity v_A at the lowest point should be in such a way that v_B should be Ã-rg . (i.e) the motion in a vertical circle is possible only if v_B > Ã- [ rg ] .

The velocity v_A of the body at the bottom point A can be obtained by using law of conservation of energy. When the stone rises from A to B, i.e through a height 2r, its potential energy increases by an amount equal to the decrease in kinetic energy. Thus,

(Potential energy at A + Kinetic energy at A ) = (Potential energy at B + Kinetic energy at B)

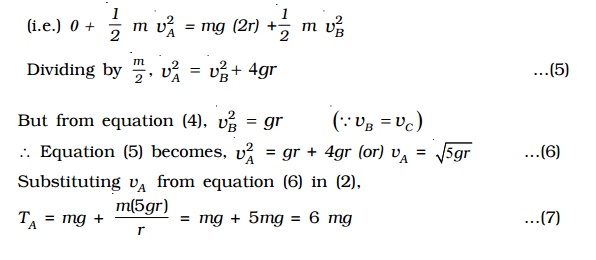
(i.e.) 0 +  1/2 m v2A = mg (2r) +1/2  m v2B

Dividing by m/2 , v2A = v2B + 4gr     .....(5)

But from equation (4), v2B = gr                 (∵vB= vC )

∴ Equation (5) becomes, 

v2A = gr + 4gr

(or) vA = Ã-[5gr] ...(6)

Substituting vA  from equation (6) in (2),

TA = mg + [m (5 gr) /r ] = mg + 5mg = 6 mg ...(7)

While rotating in a vertical circle, the stone must have a velocity greater than Ã-[5gr] or tension greater than 6mg at the lowest point, so that its velocity at the top is greater than Ã-(gr) or tension > 0.

An aeroplane while looping a vertical circle must have a velocity greater than Ã-[5gr] at the lowest point, so that its velocity at the top is greater than Ã-[gr]. In that case, pilot sitting in the aeroplane will not fall.

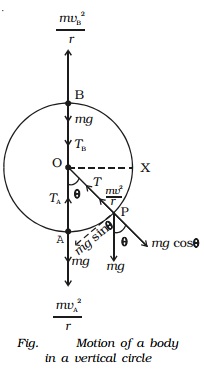
(ii) Motion on a level circular road

When a vehicle goes round a level curved path, it should be acted upon by a centripetal force. While negotiating the curved path, the wheels of the car have a tendency to leave the curved path and regain the straight-line path. Frictional force between the tyres and the road opposes this tendency of the wheels. This frictional force, therefore, acts towards the centre of the circular path and provides the necessary centripetal force.

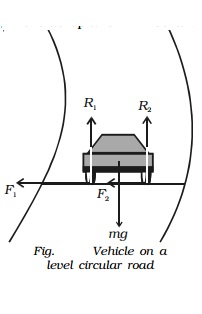
In Fig., weight of the vehicle mg acts vertically downwards. R₁, R₂ are the forces of normal reaction of the road on the wheels. As the road is level (horizontal), R₁, R₂ act vertically upwards. Obviously,

R1 + R2 = mg ...(1)

Let m * be the coefficient of friction between the tyres and the road, F₁ and F₂ be the forces of friction between the tyres and the road, directed towards the centre of the curved path.

∴ F1 = mR1 and F2 = mR2 ...(2)

If v is velocity of the vehicle while negotiating the curve, the centripetal force required = mv²/r .

As this force is provided only by the force of friction.

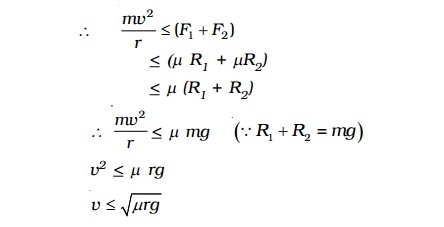
Hence the maximum velocity with which a car can go round a level curve without skidding is v = Ã-(mrg) . The value of v depends on radius r of the curve and coefficient of friction m between the tyres and the road.

(iii)Banking of curved roads and tracks

When a car goes round a level curve, the force of friction between the tyres and the road provides the necessary centripetal force. If the frictional force, which acts as centripetal force and keeps the body moving along the circular road is not enough to provide the necessary centripetal force, the car will skid. In order to avoid skidding, while going round a curved path the outer edge of the road is raised above the level of the inner edge. This is known as banking of curved roads or tracks.

Bending of a cyclist round a curve

A cyclist has to bend slightly towards the centre of the circular track in order to take a safe turn without slipping.

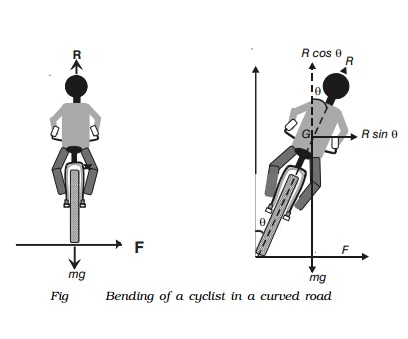
Fig. shows a cyclist taking a turn towards his right on a circular path of radius r. Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle Î¸. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components: (i) the component R sin Î¸, acting towards the centre of the curve providing necessary centripetal force for circular motion and (ii) the component R cos Î¸, balancing the weight of the cyclist along with the bicycle.

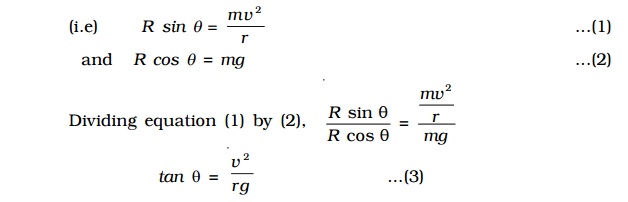
(i.e) R sin θ =  mv2/r ...(1)

and R cos θ = mg ...(2)

Dividing equation (1) by (2),

Rsin θ/R cos θ = (mv2/r ) / mg

 tan θ =  v2/rg ...(3)

Thus for less bending of cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger.

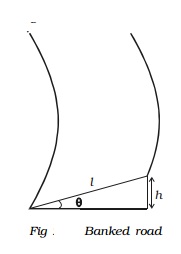
For a banked road (Fig.), let h be the elevation of the outer edge of the road above the inner edge and l be the width of the road then,

sin θ = h/l ...(4)

For small values of Î¸, sin Î¸ = tan Î¸

Therefore from equations (3) and (4)

tan θ =  h/l = v2/rg

Obviously, a road or track can be banked correctly only for a particular speed of the vehicle. Therefore, the driver must drive with a particular speed at the circular turn. If the speed is higher than the desired value, the vehicle tends to slip outward at the turn but then the frictional force acts inwards and provides the additional centripetal force. Similarly, if the speed of the vehicle is lower than the desired speed it tends to slip inward at the turn but now the frictional force acts outwards and reduces the centripetal force.

Condition for skidding

When the centripetal force is greater than the frictional force, skidding occurs. If ? is the coefficient of friction between the road and tyre, then the limiting friction (frictional force) is f = ?R where normal reaction R = mg

∴f = m (mg)

Thus for skidding,

Centripetal force > Frictional force

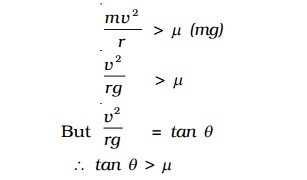
mv2/r  > m (mg)

v2/rg  > m

But v2/rg=tan Î¸

∴ tan θ > m

(i.e) when the tangent of the angle of banking is greater than the coefficient of friction, skidding occurs.