Motion in a vertical circle

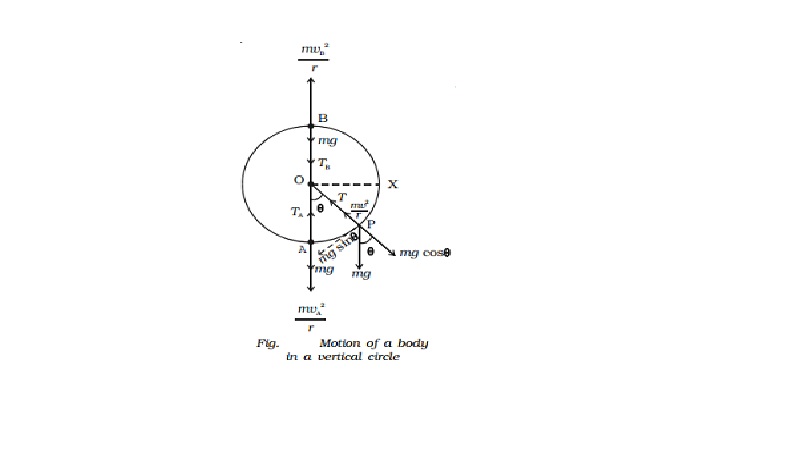
Motion in a vertical circle

Let us consider a body of mass m tied to one end of the string which is fixed at O and it is moving in a vertical circle of radius r about the point O as shown in Fig. 2.41. The motion is circular but is not uniform, since the body speeds up while coming down and slows down while going up.

Suppose the body is at P at any instant of time t, the tension T in the string always acts towards 0.

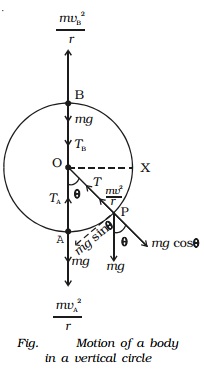
The weight mg of the body at P is resolved along the string as mg cos Î¸ which acts outwards and mg sin Î¸, perpendicular to the string.

When the body is at P, the following forces acts on it along the string.

i.          mg cos Î¸ acts along OP (outwards)

ii.            tension T acts along PO (inwards)

Net force on the body at P acting along PO = T - mg cos Î¸

This must provide the necessary centripetal force mv/r2 .

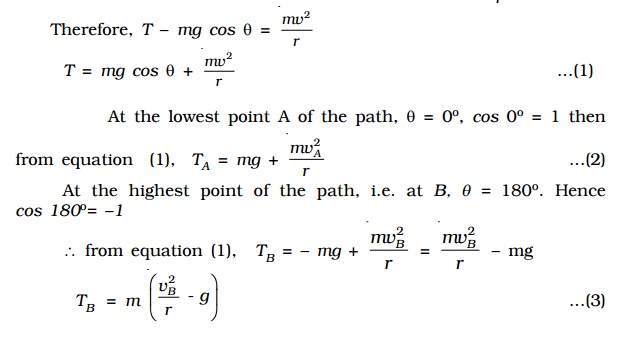
If TB > 0, then the string remains taut while if TB < 0, the string slackens and it becomes impossible to complete the motion in a vertical circle.

If the velocity vB is decreased, the tension TB in the string also decreases, and becomes zero at a certain minimum value of the speed called critical velocity. Let vC be the minimum value of the velocity, then at vB = vc , TB = 0. Therefore from equation (3),

mv2C/r - mg = 0  (or) v2C = rg

vc = root[rg]

If the velocity of the body at the highest point B is below this critical velocity, the string becomes slack and the body falls downwards instead of moving along the circular path. In order to ensure that the velocity vB at the top is not lesser than the critical velocity Ã-[ rg ], the minimum velocity vA at the lowest point should be in such a way that vB should be Ã-rg . (i.e) the motion in a vertical circle is possible only if vB > Ã- [ rg ] .

The velocity vA of the body at the bottom point A can be obtained by using law of conservation of energy. When the stone rises from A to B, i.e through a height 2r, its potential energy increases by an amount equal to the decrease in kinetic energy. Thus,

(Potential energy at A + Kinetic energy at A ) = (Potential energy at B + Kinetic energy at B)

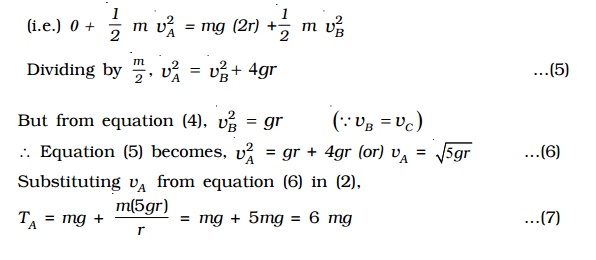
(i.e.) 0 +  1/2 m v2A = mg (2r) +1/2  m v2B

Dividing by m/2 , v2A = v2B + 4gr     .....(5)

But from equation (4), v2B = gr                 (∵vB= vC )

∴ Equation (5) becomes, 

v2A = gr + 4gr

(or) vA = Ã-[5gr] ...(6)

Substituting vA  from equation (6) in (2),

TA = mg + [m (5 gr) /r ] = mg + 5mg = 6 mg ...(7)

While rotating in a vertical circle, the stone must have a velocity greater than Ã-[5gr] or tension greater than 6mg at the lowest point, so that its velocity at the top is greater than Ã-(gr) or tension > 0.

An aeroplane while looping a vertical circle must have a velocity greater than Ã-[5gr] at the lowest point, so that its velocity at the top is greater than Ã-[gr]. In that case, pilot sitting in the aeroplane will not fall.