Multiplication of two vectors

Multiplication of two vectors

Multiplication of a vector by another vector does not follow the laws of ordinary algebra. There are two types of vector multiplication

(i) Scalar product and (ii) Vector product.

(i) Scalar product or Dot product of two vectors

If the product of two vectors is a scalar, then it is called scalar product. If  Vector A and  Vector B are two vectors, then their scalar product is written as  Vector A.

 Vector  B and read as  Vector  A dot  Vector B. Hence scalar product is also called dot product. This is also referred as inner or direct product.

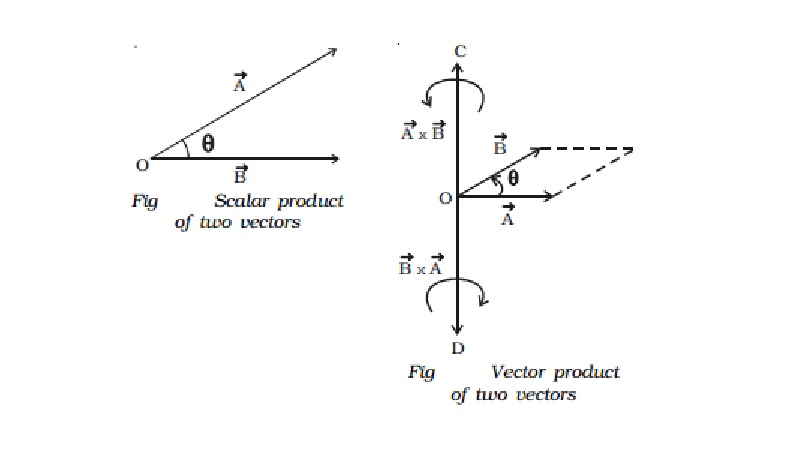
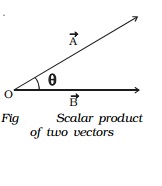
The scalar product of two vectors is a scalar, which is equal to the product of magnitudes of the two vectors and the cosine of the angle between them. The scalar product of two vectors  Vector A and  Vector B may be expressed as  Vector A .  Vector B = | Vector A| | Vector B| cos θ where |  Vector A| and |  Vector  B| are the magnitudes of  Vector A and  Vector B respectively and θ is the angle between  Vector A and  Vector B as shown in Fig.

(ii)   Vector product or Cross product of two vectors

The vector product or cross product of two vectors is a vector whose magnitude is equal to the product of their magnitudes and the sine of the smaller angle between them and the direction is perpendicular to a plane containing the two vectors.

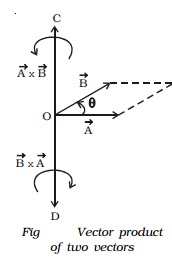
If θ is the smaller angle through which  Vector  A should be rotated to reach Vector B, then the cross product of   Vector  A and  Vector B (Fig.) is expressed as,

 Vector A x  Vector B = | Vector A| | Vector B| sin θ ^n =  Vector C

where | Vector A| and | Vector B| are the magnitudes of  Vector A and  Vector

B respectively.  Vector C is perpendicular to the plane containing  Vector A and Vector B. The direction of  Vector C is along the direction in which the tip of a screw moves when it is rotated from  Vector A to  Vector B. Hence  Vector C acts along OC. By the same argument,  Vector B ?  Vector A acts along OD.