Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Conservative forces and non-conservative forces
Conservative forces and non-conservative forces
Conservative forces
If the work done by a force in moving a body between two positions is independent of the path followed by the body, then such a force is called as a conservative force.
Examples : force due to gravity, spring force and elastic force.
The work done by the conservative forces depends only upon the initial and final position of the body.
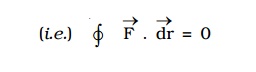
The work done by a conservative force around a closed path is zero.
Non conservative forces
Non-conservative force is the force, which can perform some resultant work along an arbitrary closed path of its point of application.
The work done by the non-conservative force depends upon the path of the displacement of the body
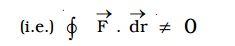
(e.g) Frictional force, viscous force, etc.
Law of conservation of energy
The law states that, if a body or system of bodies is in motion under a conservative system of forces, the sum of its kinetic energy and potential energy is constant.
Explanation
From the principle of work and energy,
Work done = change in the kinetic energy
( i.e) W1â†'2 = Ek2 - Ek1 ...(1)
If a body moves under the action of a conservative force, work done is stored as potential energy.
W1â†'2 = - (EP2 - EP1) ...(2)
Work done is equal to negative change of potential energy.
Combining the equation (1) and (2),
Ek2 - Ek1 = -(EP2 - EP1) (or) EP1 + Ek1 = EP2 + Ek2 ...(3)
which means that the sum of the potential energy and kinetic energy of a system of particles remains constant during the motion under the action of the conservative forces.
Power
It is defined as the rate at which work is done.
power = work done/ time
Its unit is watt and dimensional formula is ML2 T-3.
Power is said to be one watt, when one joule of work is said to be done in one second.
If dw is the work done during an interval of time dt then,
power = dw/ dt ...(1)
But dw = (F cos θ) ds ...(2)
where θ is the angle between the direction of the force and displacement. F cos θ is component of the force in the direction of the small displacement ds.
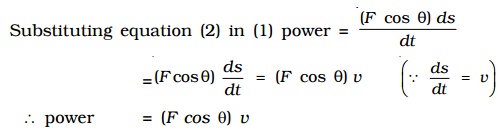
Substituting equation (2) in (1)
power = (F cos θ) ds / dt
=( F cosθ) ds / dt= F( cos θ) v
∴ power = (F cos θ) v
If F and v are in the same direction, then
power = F v cos 0 = F v = Force x velocity
It is also represented by the dot product of F and v.
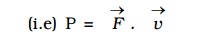
Related Topics