Principle of work and energy (work - energy theorem) Statement

Principle of work and energy (work - energy theorem) Statement

The work done by a force acting on the body during its displacement is equal to the change in the kinetic energy of the body during that displacement.

Proof

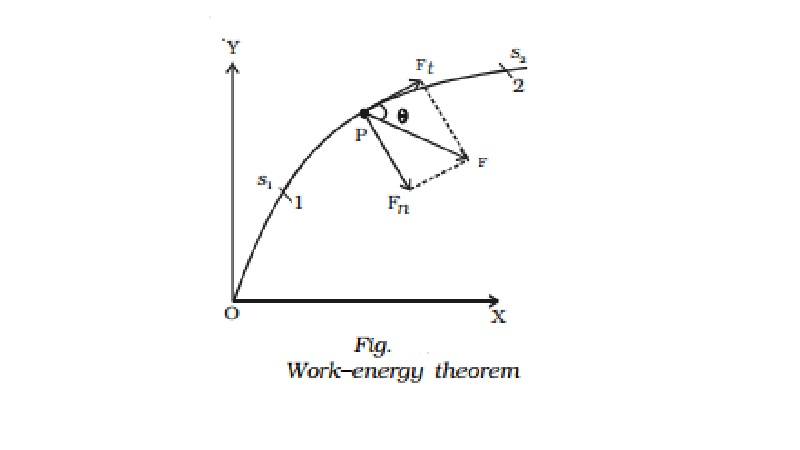
Let us consider a body of mass m acted upon by a force F and moving with a velocity v along a path as shown in Fig.. At any instant, let P be the position of the body from the origin O. Let θ be the angle made by the direction of the force with the tangential line drawn at P.

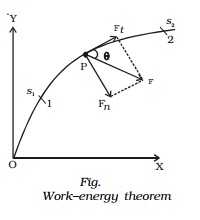
The force F can be resolved into two rectangular components :

(i) Ft  = F cos θ , tangentially and

(ii) Fn = F sin θ , normally at P.

But Ft  = mat ...(1)

where at  is the acceleration of the body in the tangential direction

∴ F cos θ = mat ...(2)

But at  = dv/dt ...(3)

∴ substituting equation (3) in (2),

F cos θ = m dv/dt = m dv/ds .ds/dt ...(4)

F cosθ ds = mv dv ...(5)

where ds is the small displacement.

Let v1 and v2 be the velocities of the body at the positions 1 and 2 and the corresponding distances be s1 and s2.

Integrating the equation (5),

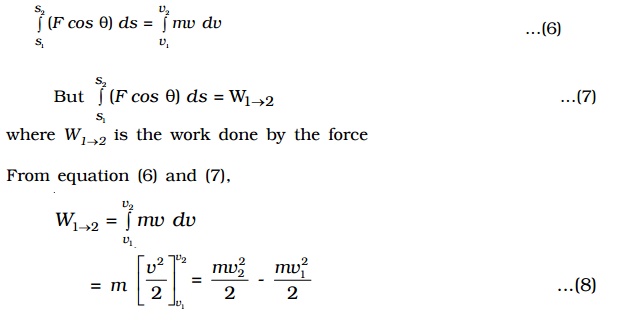
Therefore work done

= final kinetic energy âˆ' initial kinetic energy

= change in kinetic energy

This is known as Work-energy theorem.