Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Collision: Types - Elastic collision and Inelastic collision
Collisions
A collision between two particles is said to occur if they physically strike against each other or if the path of the motion of one is influenced by the other. In physics, the term collision does not necessarily mean that a particle actually strikes. In fact, two particles may not even touch each other and yet they are said to collide if one particle influences the motion of the other.
When two bodies collide, each body exerts a force on the other. The two forces are exerted simultaneously for an equal but short interval of time. According to Newton?s third law of motion, each body exerts an equal and opposite force on the other at each instant of collision. During a collision, the two fundamental conservation laws namely, the law of conservation of momentum and that of energy are obeyed and these laws can be used to determine the velocities of the bodies after collision.
Collisions are divided into two types : (i) elastic collision and (ii) inelastic collision
Elastic collision
If the kinetic energy of the system is conserved during a collision, it is called an elastic collision. (i.e) The total kinetic energy before collision and after collision remains unchanged. The collision between subatomic particles is generally elastic. The collision between two steel or glass balls is nearly elastic. In elastic collision, the linear momentum and kinetic energy of the system are conserved.
Elastic collision in one dimension
If the two bodies after collision move in a straight line, the collision is said to be of one dimension.
Consider two bodies A and B of masses m1 and m2 moving along the same straight line in the same direction with velocities u1 and u2respectively as shown in Fig.. Let us assume that u1 is greater than u2. The bodies A and B suffer a head on collision when they strike and continue to move along the same straight line with velocities v1 and v2 respectively.
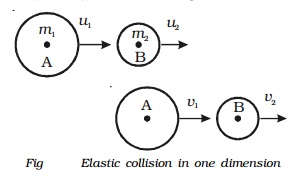
From the law of conservation of linear momentum,
Total momentum before collision = Total momentum after collision
m1u1 + m2u2 = m1v1 + m2v2 ...(1)
Since the kinetic energy of the bodies is also conserved during the collision
Total kinetic energy before collision = Total kinetic energy after collision
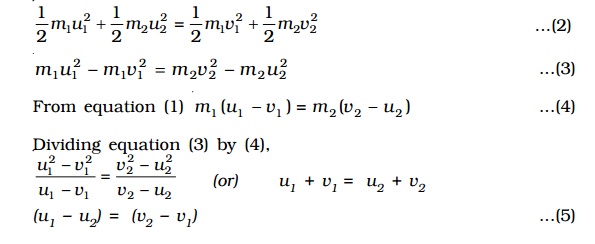
Equation 5 shows that in an elastic one-dimensional collision, the relative velocity with which the two bodies approach each other before collision is equal to the relative velocity with which they recede from each other after collision.
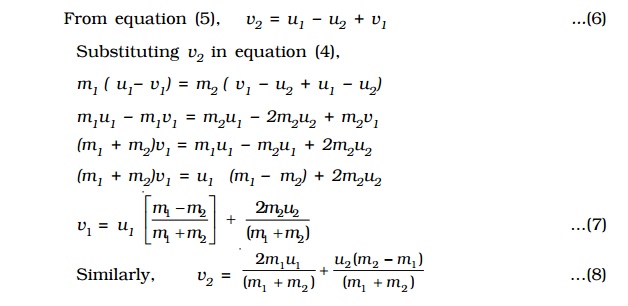
Special cases
Case ( i) : If the masses of colliding bodies are equal, i.e. m1 = m2
v1 = u2 and v2 = u1 .
After head on elastic collision, the velocities of the colliding bodies
are mutually interchanged.
Case (ii) : If the particle B is initially at rest, (i.e) u2 = 0 then
v1 = ( mA-mB / mA+mB) / uA
v2 = ( 2mA / mA+mB) / u1
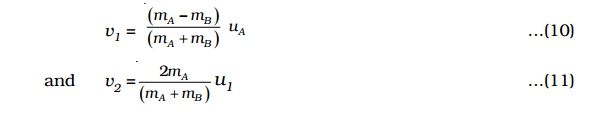
Inelastic collision
During a collision between two bodies if there is a loss of kinetic energy, then the collision is said to be an inelastic collision. Since there is always some loss of kinetic energy in any collision, collisions are generally inelastic. In inelastic collision, the linear momentum is conserved but the energy is not conserved. If two bodies stick together, after colliding, the collision is perfectly inelastic but it is a special case of inelastic collision called plastic collision. (eg) a bullet striking a block of wood and being embedded in it. The loss of kinetic energy usually results in the form of heat or sound energy.
Let us consider a simple situation in which the inelastic head on collision between two bodies of masses mA and mB takes place. Let the colliding bodies be initially move with velocities u1 and u2. After collision both bodies stick together and moves with common velocity v.
Total momentum of the system before collision = mAu1 + mBu2
Total momentum of the system after collision =
mass of the composite body ? common velocity = (mA+ mB ) v By law of conservation of momentum
mAu1 + mBu2 = (mA+ mB) v
(or)
v = mAuA + mB uB / mA + mB
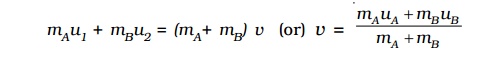
Thus, knowing the masses of the two bodies and their velocities before collision, the common velocity of the system after collision can be calculated.
If the second particle is initially at rest i.e. u2 = 0 then

v = mAuA / (mA+mB)
kinetic energy of the system before collision
EK1 = 1/2 m AuA2 [u2 = 0]
and kinetic energy of the system after collision
EK2 = 1/2(mA +mB )v2
Hence,
Ek2/Ek1 = kinetic energy after collision / kinetic energy before collision
= ( mA+mB)v2 / mAuA2
Substituting the value of v in the above equation,
Ek2/Ek1 = mA/mA+mB
(Or)
Ek2/Ek1 < 1
It is clear from the above equation that in a perfectly inelastic collision, the kinetic energy after impact is less than the kinetic energy before impact. The loss in kinetic energy may appear as heat energy.
Related Topics