Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Centre of mass

Centre of mass
Every body is a collection of large number of tiny particles. In translatory motion of a body, every particle experiences equal displacement with time; therefore the motion of the whole body may be represented by a particle. But when the body rotates or vibrates during translatory motion, then its motion can be represented by a point on the body that moves in the same way as that of a single particle subjected to the same external forces would move. A point in the system at which whole mass of the body is supposed to be concentrated is called centre of mass of the body. Therefore, if a system contains two or more particles, its translatory motion can be described by the motion of the centre of mass of the system.
Centre of mass of a two-particle system
Let us consider a system consisting of two particles of masses m1 and m2. P1 and P2 are their positions at time t and r1 and r 2 are the corresponding distances from the origin O as shown in Fig.. Then the velocity and acceleration of the particles are,
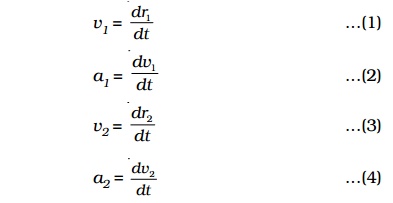
v1 = dr1/dt .....(1)
a1 = dr1/dt .....(2)
v2 = dr2/dt .....(3)
a2 = dr2/dt .....(4)
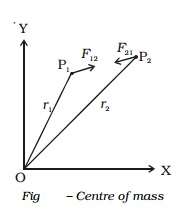
The particle at P1 experiences two forces :
(i) a force F12 due to the particle at P2 and
(ii) force F1e , the external force due to some particles external to the system.
If F1 is the resultant of these two forces,
F1 = F12 + F1e
Similarly, the net force F2 acting on the particle P2 is,
F2 = F21 + F2e
where F21 is the force exerted by the particle at P1 on P2 By using Newton?s second law of motion,
F1 = m1a1 .......(7)
and F2= m2a2
Adding equations (7) and (8), m1a1 + m2a2 = F1 + F2 Substituting F1 and F2 from (5) and (6)
m1a1 + m2a2 = F12 + F1e+ F21 + F2e
By Newton's third law, the internal force F12 exerted by particle at P2 on the particle at P1 is equal and opposite to F21, the force exerted by particle at P1 on P2.
(i.e) F12 = - F21
F = F1e+ F2e
[∵m1a1 + m 2a 2 = F ]
where F is the net external force acting on the system.
The total mass of the system is given by,
M = m1+m2
Let the net external force F acting on the system produces an acceleration aCM called the acceleration of the centre of mass of the system
By Newton's second law, for the system of two particles,
F = M aCM
From (10) and (12), M aCM = m1a1+m2a2
Let RCM be the position vector of the centre of mass.
∴aCM =d2(RCM) / dt2
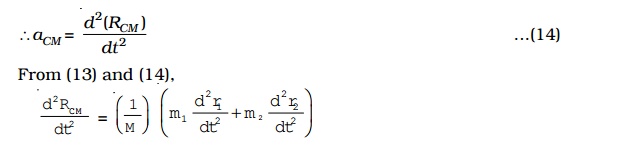
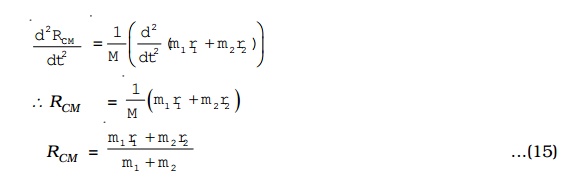
∴ RCM = 1/M(m1r1+m2r2)
∴ RCM = (m1r1+m2r2) / m1+m2
This equation gives the position of the centre of mass of a system comprising two particles of masses m1 and m2
If the masses are equal (m1 = m2), then the position vector of the centre of mass is,
RCM = ( r1 + r2 ) / 2

which means that the centre of mass lies exactly in the middle of the line joining the two masses.
Centre of mass of a body consisting of n particles
For a system consisting of n particles with masses m1, m2, m3 ,.... mn with position vectors r1, r2, r3,....rn, the total mass of the system is,
M = m1 + m2 +m3 +..........+mn
The position vector RCM of the centre of mass with respect to origin O is given by
RCM= m1 r1 + m 2 r2 .....+ m n rn / m1 + m 2 + mn

x = m1 x1 + m2 x 2 + .....mn xn / m1 + m 2 + mn
and y = m 1 y 1 + m 2 y 2 + .....m n yn / m 1 + m 2 +m n
Example for motion of centre of mass
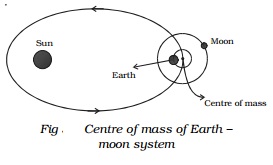
Let us consider the motion of the centre of mass of the Earth and moon system (Fig). The moon moves round the Earth in a circular orbit and the Earth moves round the Sun in an elliptical orbit. It is more correct to say that the Earth and the moon both move in circular orbits about their common centre of mass in an elliptical orbit round the Sun.
For the system consisting of the Earth and the moon, their mutual gravitational attractions are the internal forces in the system and Sun?s attraction on both the Earth and moon are the external forces acting on the centre of mass of the system.
Related Topics