Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Uniform circular motion
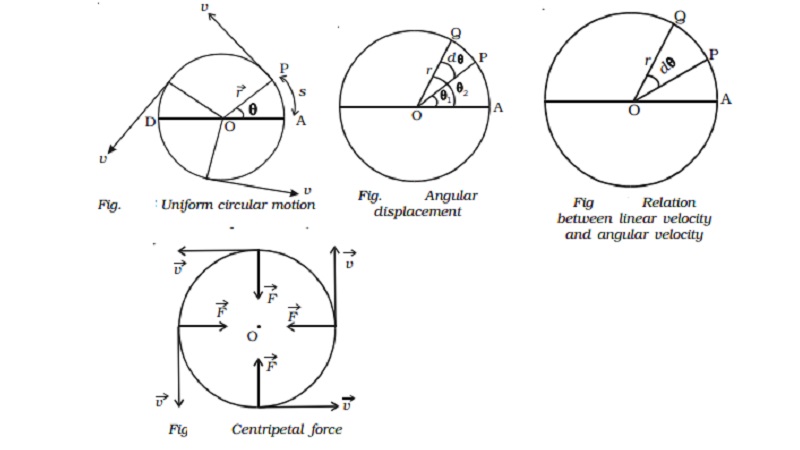
Uniform circular motion
The revolution of the Earth around the Sun, rotating fly wheel, electrons revolving around the nucleus, spinning top, the motion of a fan blade, revolution of the moon around the Earth etc. are some examples of circular motion. In all the above cases, the bodies or particles travel in a circular path. So, it is necessary to understand the motion of such bodies.
When a particle moves on a circular path with a constant speed, then its motion is known as uniform circular motion in a plane. The magnitude of velocity in circular motion remains constant but the direction changes continuously.

Let us consider a particle of mass m moving with a velocity v along the circle of radius r with centre O as shown in Fig. P is the position of the particle at a given instant of time such that the radial line OP makes an angle θ with the reference line DA. The magnitude of the velocity remains constant, but its direction changes continuously. The linear velocity always acts tangentially to the position of the particle (i.e) in each position, the linear velocity Vector v is perpendicular to the radius vector Vector r.
Angular displacement
Let us consider a particle of mass m moving along the circular path of radius r as shown in Fig.. Let the initial position of the particle be A. P and Q are the positions of the particle at any instants of time t and t + dt respectively. Suppose the particle traverses a distance ds along the circular path in time interval dt. During this interval, it moves through an angle dθ = θ2 �' θ1. The angle swept by the radius vector at a given time is called the angular displacement of the particle.
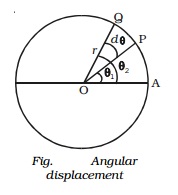
If r be the radius of the circle, then the angular displacement is given by dθ = ds/r . The angular displacement is measured in terms of radian.
Angular velocity
The rate of change of angular displacement is called the angular velocity of the particle.
Let dθ be the angular displacement made by the particle in time dt , then the angular velocity of the particle is dθ /dt ω = . Its unit is rad s-1 and dimensional formula is T-1.
For one complete revolution, the angle swept by the radius vector is 360o or 2π radians. If T is the time taken for one complete revolution, known as period, then the angular velocity of the particle is
ω= θ/t = 2 π/T .
If the particle makes n revolutions per second, then ω=2π(1/T) = 2πn
where n = 1/T is the frequency of revolution.
Relation between linear velocity and angular velocity
Let us consider a body P moving along the circumference of a circle of radius r with linear velocity v and angular velocity ω as shown in Fig.. Let it move from P to Q in time dt and dθ be the angle swept by the radius vector.
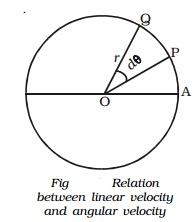
Let PQ = ds, be the arc length covered by the particle moving along the circle, then the angular displacement d θ is expressed as dθ = ds/r. But ds=vdt.
d θ/dt=v/r
(i.e) Angular velocity ω = v/r or v =ω r
In vector notation,
Vector v = Vector ω x Vector r
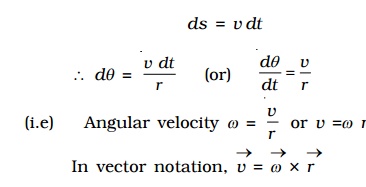
Thus, for a given angular velocity ω, the linear velocity v of the particle is directly proportional to the distance of the particle from the centre of the circular path (i.e) for a body in a uniform circular motion, the angular velocity is the same for all points in the body but linear velocity is different for different points of the body.
Angular acceleration
If the angular velocity of the body performing rotatory motion is non-uniform, then the body is said to possess angular acceleration.
The rate of change of angular velocity is called angular acceleration.
If the angular velocity of a body moving in a circular path changes from ω1 to ω2 in time t then its angular acceleration is
α= d ω/dt = ( ω2 - ω1 )/t
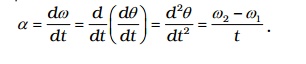
The angular acceleration is measured in terms of rad s�'2 and its dimensional formula is T �' 2.
Relation between linear acceleration and angular acceleration
If dv is the small change in linear velocity in a time interval dt then linear acceleration is
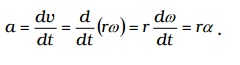
= d v/dt = d (r ω)/dt = ra
Centripetal acceleration
The speed of a particle performing uniform circular motion remains constant throughout the motion but its velocity changes continuously due to the change in direction (i.e) the particle executing uniform circular motion is said to possess an acceleration.
Consider a particle executing circular motion of radius r with linear velocity v and angular velocity ω. The linear velocity of the particle acts along the tangential line. Let dθ be the angle described by the particle at the centre when it moves from A to B in time dt.
At A and B, linear velocity v acts along AH and BT respectively. In Fig. ∠ AOB =dθ = ∠HET (∵ angle subtended by the two radii of a circle = angle subtended by the two tangents).
The velocity v at B of the particle makes an angle dθ with the line BC and hence it is resolved horizontally as v cos dθ along BC and vertically as v sin d θ along BD.
∴ The change in velocity along the horizontal direction = v cos dθ -v
If dθ is very small, cos dθ = 1
∴ Change in velocity along the horizontal direction = v �' v = 0
(i.e) there is no change in velocity in the horizontal direction.
The change in velocity in the vertical direction (i.e along AO) is
dv = v sin dθ �' 0 = v sin dθ
If dθ is very small, sin dθ = dθ
∴ The change in velocity in the vertical direction (i.e) along radius of the circle
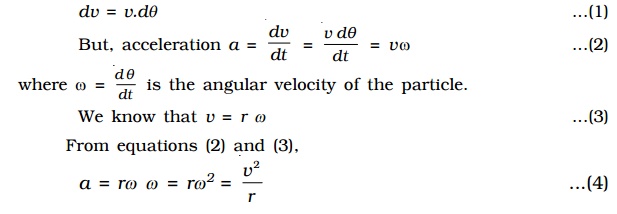
dv = v.dθ ...(1)
But, acceleration a = dv/dt = v dθ/dt = vω ...(2)
where ω = dθ/dt is the angular velocity of the particle.
We know that v = r ω ...(3)
From equations (2) and (3),
a = rω ω = rω2 = v2/r ...(4)
Hence, the acceleration of the particle producing uniform circular motion is equal to v2/r and is along AO (i.e) directed towards the centre of the circle. This acceleration is directed towards the centre of the circle along the radius and perpendicular to the velocity of the particle. This acceleration is known as centripetal or radial or normal acceleration.
Centripetal force
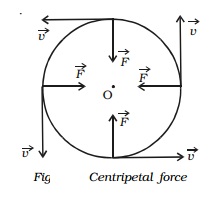
According to Newton's first law of motion, a body possesses the property called directional inertia (i.e) the inability of the body to change its direction. This means that without the application of an external force, the direction of motion can not be changed. Thus when a body is moving along a circular path, some force must be acting upon it, which continuously changes the body from its straight-line path (Fig). It makes clear that the applied force should have no component in the direction of the motion of the body or the force must act at every point perpendicular to the direction of motion of the body. This force, therefore, must act along the radius and should be directed towards the centre.

Hence for circular motion, a constant force should act on the body, along the radius towards the centre and perpendicular to the velocity of the body. This force is known as centripetal force.
If m is the mass of the body, then the magnitude of the centripetal force is given by
F = mass x centripetal acceleration
=m (rω2)
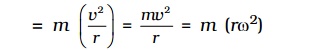
Examples
Any force like gravitational force, frictional force, electric force, magnetic force etc. may act as a centripetal force. Some of the examples of centripetal force are :
i. In the case of a stone tied to the end of a string whirled in a circular path, the centripetal force is provided by the tension in the string.
ii. When a car takes a turn on the road, the frictional force between the tyres and the road provides the centripetal force.
iii. In the case of planets revolving round the Sun or the moon revolving round the earth, the centripetal force is provided by the gravitational force of attraction between them
iv. For an electron revolving round the nucleus in a circular path, the electrostatic force of attraction between the electron and the nucleus provides the necessary centripetal force.
Centrifugal reaction
According to Newton's third law of motion, for every action there is an equal and opposite reaction. The equal and opposite reaction to the centripetal force is called centrifugal reaction, because it tends to take the body away from the centre. In fact, the centrifugal reaction is a pseudo or apparent force, acts or assumed to act because of the acceleration of the rotating body.
In the case of a stone tied to the end of the string is whirled in a circular path, not only the stone is acted upon by a force (centripetal force) along the string towards the centre, but the stone also exerts an equal and opposite force on the hand (centrifugal force) away from the centre, along the string. On releasing the string, the tension disappears and the stone flies off tangentially to the circular path along a straight line as enuciated by Newton's first law of motion.
When a car is turning round a corner, the person sitting inside the car experiences an outward force. It is because of the fact that no centripetal force is supplied by the person. Therefore, to avoid the outward force, the person should exert an inward force.
Related Topics