Relation between linear velocity and angular velocity

Angular velocity

The rate of change of angular displacement is called the angular velocity of the particle.

Let dθ be the angular displacement made by the particle in time dt , then the angular velocity of the particle is dθ /dt ω = . Its unit is rad s-1 and dimensional formula is T-1.

For one complete revolution, the angle swept by the radius vector is 360o or 2π radians. If T is the time taken for one complete revolution, known as period, then the angular velocity of the particle is

ω= θ/t = 2 π/T .

If the particle makes n revolutions per second, then ω=2π(1/T) = 2πn

where n = 1/T  is the frequency of revolution.

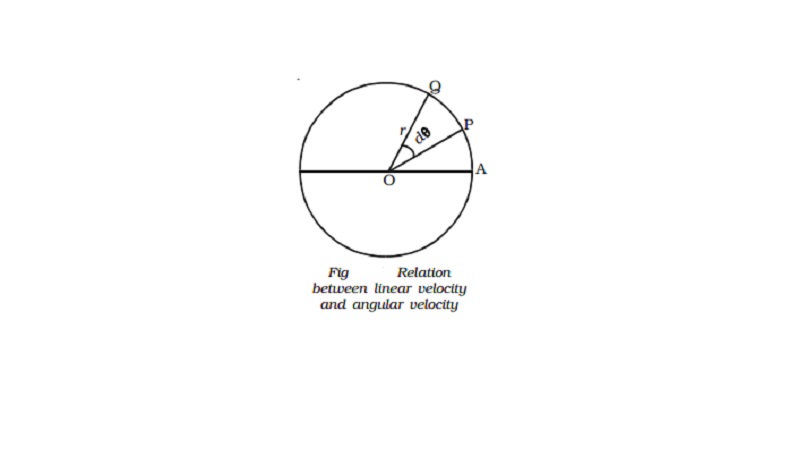
Relation between linear velocity and angular velocity

Let us consider a body P moving along the circumference of a circle of radius r with linear velocity v and angular velocity ω as shown in Fig.. Let it move from P to Q in time dt and dθ be the angle swept by the radius vector.

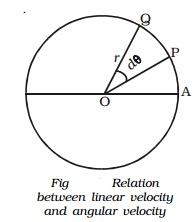
Let PQ = ds, be the arc length covered by the particle moving along the circle, then the angular displacement d θ is expressed as dθ = ds/r. But ds=vdt.

d θ/dt=v/r

(i.e) Angular velocity ω = v/r or v =ω r

In vector notation,

Vector v = Vector ω x Vector r

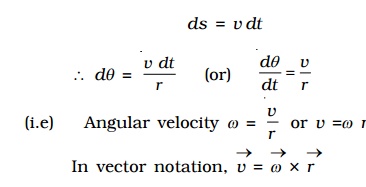
Thus, for a given angular velocity ω, the linear velocity v of the particle is directly proportional to the distance of the particle from the centre of the circular path (i.e) for a body in a uniform circular motion, the angular velocity is the same for all points in the body but linear velocity is different for different points of the body.