Theorems of moment of inertia : Perpendicular and Parallel axes theorem

Theorems of moment of inertia

(i) Parallel axes theorem

Statement

The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of gravity and the product of the mass of the body and the square of the distance between the two axes.

Proof

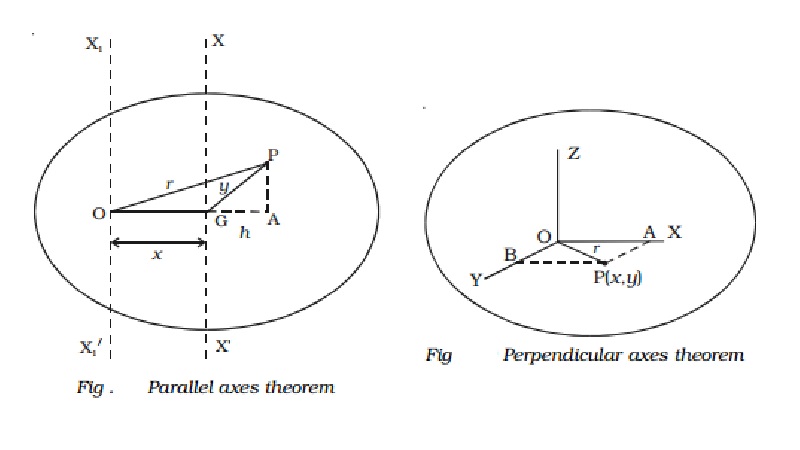
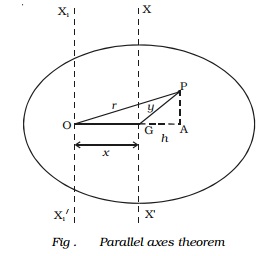
Let us consider a body having its centre of gravity at G as shown in Fig.. The axis XX′ passes through the centre of gravity and is perpendicular to the plane of the body. The axis X₁X₁′ passes through the point O and is parallel to the axis XX′ . The distance between the two parallel axes is x.

Let the body be divided into large number of particles each of mass m . For a particle P at a distance r from O, its moment of inertia about the axis X₁OX₁′ is equal to m r ².

The moment of inertia of the whole body about the axis X₁X₁′ is given by,

I = Σ mr²  ???(1)

From the point P, drop a perpendicular PA to the extended OG and join PG.

In the ∆OPA,

OP ² = OA² + AP ²

r² = x² + 2xh + h² + AP²  ???(2)

But from ∆ GPA,

GP ² = GA² + AP ²

y ² = h ² + AP ²  ..(3)

Substituting equation (3) in (2),

r ² = x ² + 2xh + y ²   ..(4)

Substituting equation (4) in (1),

I₀   = Σ m (x² + 2xh + y²)

= Σmx² + Σ2mxh + Σmy²

= Mx² + My² + 2xΣmh

Here My² = I_G is the moment of inertia of the body about the line passing through the centre of gravity. The sum of the turning moments of all the particles about the centre of gravity is zero, since the body is balanced about the centre of gravity G.

Σ (mg) (h) = 0  (or)  Σ mh = 0 [since g is a constant]

equation (5) becomes, I₀= Mx² + I_G

Thus the parallel axes theorem is proved.

(ii) Perpendicular axes theorem

Statement

The moment of inertia of a plane laminar body about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.

Proof

Consider a plane lamina having the axes OX and OY in the plane of the lamina as shown Fig. The axis OZ passes through O and is perpendicular to the plane of the lamina. Let the lamina be divided into a large number of particles, each of mass m. A particle at P at a distance r from O has coordinates (x,y).

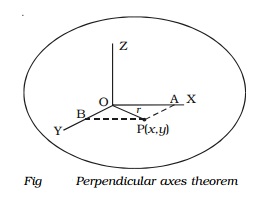
∴r² = x²+y²

The moment of inertia of the particle P about the axis OZ = m r². The moment of inertia of the whole lamina about the axis OZ is

I _Z= Σmr²

The moment of inertia of the whole lamina about the axis OX is

I_x =Σ my ²

Similarly, I _y= Σ  mx ²

From eqn. (2),   I = Σ mr² = Σ m(x²+y²)

I = Σmx²+ Σ my² = I_x+ I_y

 I_z = I_x+ I_y

which proves the perpendicular axes theorem.

List : Moment of Inertia of different bodies

Body :        Axis of Rotation

Thin Uniform Rod        

          Axis passing through its         centre  of  gravity  and   perpendicular to its length

          Axis passing through the        end and perpendicular to         its length.

Thin Circular Ring        

          Axis passing through its         centre and perpendicular         to its plane.

          Axis passing through its         Diameter

          Axis passing through a Tangent

Circular Disc       

           Axis passing through its        centre and perpendicular         to its plane.

          Axis passing through its         diameter

          Axis passing through a tangent

Solid Sphere        

          Axis passing through its         diameter

          Axis passing through a tangent

Solid Cylinder     

          Its own axis         

          Axis passing through its         centre and perpedicular to       its length