Solving Equilibrium Problems: pH of a Monoprotic Weak Acid

pH of a Monoprotic Weak Acid

To illustrate the systematic approach, let us calculate the pH of 1.0 M HF. Two equilbria affect the pH of this system. The first, and most obvious, is the acid disso- ciation reaction for HF

HF(aq)+ H₂O(l)   < = = >   H₃O+(aq)+ F–(aq)

for which the equilibrium constant expression is

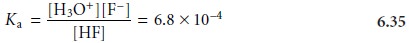
The second equilibrium reaction is the dissociation of water, which is an obvious yet easily disregarded reaction

2H₂O(l)  < == == >   H₃O+(aq)+ OH–(aq)

K_w = [H₃O+][OH–] = 1.00 x 10–14            6.36

Counting unknowns, we find four ([HF], [F–], [H₃O+], and [OH–]). To solve this problem, therefore, we need to write two additional equations involving these un- knowns. These equations are a mass balance equation

C_HF = [HF]+ [F–]            6.37

and a charge balance equation

H₃O+]= [F–] + [OH–]           6.38

We now have four equations (6.35, 6.36, 6.37, and 6.38) and four unknowns ([HF], [F–], [H₃O+], and [OH–]) and are ready to solve the problem. Before doing so, however, we will simplify the algebra by making two reasonable assumptions. First, since HF is a weak acid, we expect the solution to be acidic; thus it is reason- able to assume that

[H₃O+] >> [OH–]

simplifying the charge balance equation (6.38) to

[H₃O+]= [F–]               6.39

Second, since HF is a weak acid we expect that very little dissociation occurs, and

[HF] >> [F–]

Thus, the mass balance equation (6.36) simplifies to

C_HF = [HF]                       6.40

For this exercise we will accept our assumptions if the error introduced by each as- sumption is less than ±5%.

Substituting equations 6.39 and 6.40 into the equilibrium constant expression for the dissociation of HF (equation 6.35) and solving for the concentration of H₃O+ gives us

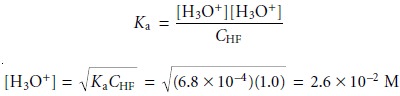
Before accepting this answer, we must verify that our assumptions are acceptable. The first assumption was that the [OH–] is significantly smaller than the [H₃O+]. To calculate the concentration of OH– we use the K_w expression (6.36)

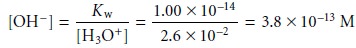
Clearly this assumption is reasonable. The second assumption was that the [F–] is significantly smaller than the [HF]. From equation 6.39 we have

[F–] = 2.6 x 10–2 M

Since the [F–] is 2.6% of C_HF, this assumption is also within our limit that the error be no more than ±5%. Accepting our solution for the concentration of H₃O+, we find that the pH of 1.0 M HF is 1.59.

How does the result of this calculation change if we require our assumptions to have an error of less than ±1%. In this case we can no longer assume that [HF] >> [F–]. Solving the mass balance equation (6.37) for [HF]

[HF] = C_HF – [F–]

and substituting into the K_a expression along with equation 6.39 gives

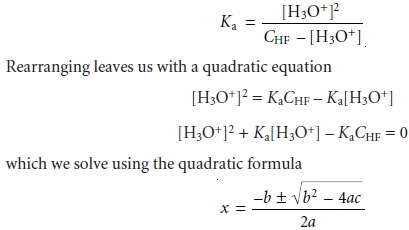
where a, b, and c are the coefficients in the quadratic equation ax2 + bx + c = 0. Solving the quadratic formula gives two roots, only one of which has any chemical significance. For our problem the quadratic formula gives roots of

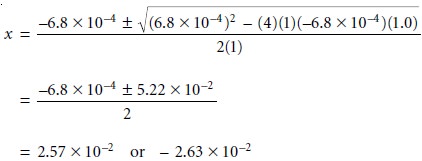
Only the positive root has any chemical significance since the negative root implies that the concentration of H₃O+ is negative. Thus, the [H₃O+] is 2.6 x 10–2 M, and the pH to two significant figures is still 1.59.

This same approach can be extended to find the pH of a monoprotic weak base, replacing K_a with K_b, C_HF with the weak base’s concentration, and solving for the [OH–] in place of [H₃O+]