Equilibrium Constants for Acid–Base Reactions

Acid–Base Reactions

A useful definition of acids and bases is that independently introduced by Jo- hannes Brønsted (1879–1947) and Thomas Lowry (1874–1936) in 1923. In the Brønsted-Lowry definition, acids are proton donors, and bases are proton accep- tors. Note that these definitions are interrelated. Defining a base as a proton accep- tor means an acid must be available to provide the proton. For example, in reac- tion 6.7 acetic acid, CH₃COOH, donates a proton to ammonia, NH₃, which serves as the base.

CH₃COOH(aq)+ NH₃(aq) < = = = = > CH₃COO–(aq)+ NH₄+(aq)            6.7

When an acid and a base react, the products are a new acid and base. For exam- ple, the acetate ion, CH₃COO–, in reaction 6.7 is a base that reacts with the acidic ammonium ion, NH₄+, to produce acetic acid and ammonia. We call the acetate ion the conjugate base of acetic acid, and the ammonium ion is the conjugate acid of ammonia.

Strong and Weak Acids 

The reaction of an acid with its solvent (typically water) is called an acid dissociation reaction. Acids are divided into two categories based on the ease with which they can donate protons to the solvent. Strong acids, such as HCl, almost completely transfer their protons to the solvent molecules.

HCl(aq)+ H₂O(l) → H₃O+(aq)+ Cl–(aq)

In this reaction H₂O serves as the base. The hydronium ion, H₃O+, is the conju- gate acid of H₂O, and the chloride ion is the conjugate base of HCl. It is the hy- dronium ion that is the acidic species in solution, and its concentration deter- mines the acidity of the resulting solution. We have chosen to use a single arrow (→) in place of the double arrows (t) to indicate that we treat HCl as if it were completely dissociated in aqueous solutions. A solution of 0.10 M HCl is effec- tively 0.10 M in H₃O+ and 0.10 M in Cl–. In aqueous solutions, the common strong acids are hydrochloric acid (HCl), hydroiodic acid (HI), hydrobromic acid (HBr), nitric acid (HNO₃), perchloric acid (HClO₄), and the first proton of sulfu- ric acid (H₂SO₄).

Weak acids, of which aqueous acetic acid is one example, cannot completely donate their acidic protons to the solvent. Instead, most of the acid remains undis- sociated, with only a small fraction present as the conjugate base.

CH₃COOH(aq)+ H₂O(l) < = = = = > H₃O+(aq)+ CH₃COO–(aq)

The equilibrium constant for this reaction is called an acid dissociation constant,

K_a, and is written as

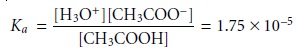
Note that the concentration of H₂O is omitted from the K_a expression because its value is so large that it is unaffected by the dissociation reaction.* The magnitude of K_a provides information about the relative strength of a weak acid, with a smaller K_a corresponding to a weaker acid. The ammonium ion, for example, with a K_a of 5.70 x 10–10, is a weaker acid than acetic acid.

Monoprotic weak acids, such as acetic acid, have only a single acidic proton and a single acid dissociation constant. Some acids, such as phosphoric acid, can donate more than one proton and are called polyprotic weak acids. Polyprotic acids are described by a series of acid dissociation steps, each characterized by it own acid dissociation constant. Phosphoric acid, for example, has three acid dissociation re- actions and acid dissociation constants.

The decrease in the acid dissociation constant from K_a1 to K_a3 tells us that each suc- cessive proton is harder to remove. Consequently, H₃PO₄ is a stronger acid than H₂PO₄–, and H PO₄– is a stronger acid than HPO₄2–.

Strong and Weak Bases 

Just as the acidity of an aqueous solution is a measure of the concentration of the hydronium ion, H₃O+, the basicity of an aqueous solution is a measure of the concentration of the hydroxide ion, OH–. The most common example of a strong base is an alkali metal hydroxide, such as sodium hydroxide, which completely dissociates to produce the hydroxide ion.

NaOH(aq) → Na+(aq)+ OH–(aq)

Weak bases only partially accept protons from the solvent and are characterized by a base dissociation constant, K_b. For example, the base dissociation reaction and base dissociation constant for the acetate ion are

Polyprotic bases, like polyprotic acids, also have more than one base dissociation re- action and base dissociation constant.

Amphiprotic Species 

Some species can behave as either an acid or a base. For ex- ample, the following two reactions show the chemical reactivity of the bicarbonate ion, HCO₃ –, in water.

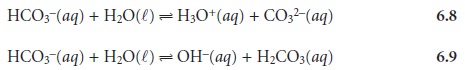
A species that can serve as both a proton donor and a proton acceptor is called am- phiprotic. Whether an amphiprotic species behaves as an acid or as a base depends on the equilibrium constants for the two competing reactions. For bicarbonate, the acid dissociation constant for reaction 6.8

K_a2 = 4.69 x 10–11

is smaller than the base dissociation constant for reaction 6.9.

K_b2 = 2.25 x 10–8

Since bicarbonate is a stronger base than it is an acid (k_b2 > k_a2), we expect that aqueous solutions of HCO3– will be basic.

Dissociation of Water 

Water is an amphiprotic solvent in that it can serve as an acid or a base. An interesting feature of an amphiprotic solvent is that it is capable of reacting with itself as an acid and a base.

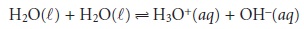
The equilibrium constant for this reaction is called water’s dissociation con- stant, K_w,

which has a value of 1.0000 x 10–14 at a temperature of 24 °C. The value of K_w varies substantially with temperature. For example, at 20 °C, K_w is 6.809 x 10–15, but at 30 °C K_w is 1.469 x 10–14. At the standard state temperature of 25 °C, K_w is 1.008 x 10–14, which is sufficiently close to 1.00 x 10–14 that the latter value can be used with negligible error.

The pH Scale 

An important consequence of equation 6.10 is that the concentra- tions of H₃O+ and OH– are related. If we know [H₃O+] for a solution, then [OH–] can be calculated using equation 6.10.

Equation 6.10 also allows us to develop a pH scale that indicates the acidity of a so- lution. When the concentrations of H₃O+ and OH– are equal, a solution is neither acidic nor basic; that is, the solution is neutral. Letting

[H₃O+] = [OH–]

and substituting into equation 6.10 leaves us with

K_w = [H₃O+]2 = 1.00 x 10–14

A neutral solution has a hydronium ion concentration of 1.00 x 10–7 M and a pH of 7.00.* For a solution to be acidic, the concentration of H₃O+ must be greater than that for OH–, or

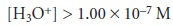
The pH of an acidic solution, therefore, must be less than 7.00. A basic solution, on the other hand, will have a pH greater than 7.00. Figure 6.3 shows the pH scale along with pH values for some representative solutions.

Tabulating Values for K_a and K_b 

A useful observation about acids and bases is that the strength of a base is inversely proportional to the strength of its conjugate acid. Consider, for example, the dissociation reactions of acetic acid and acetate.

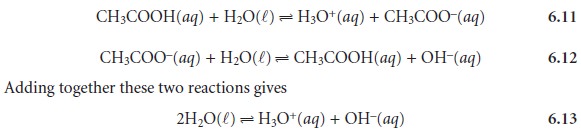
The equilibrium constant for equation 6.13 is K_w. Since equation 6.13 is obtained by adding together reactions 6.11 and 6.12, K_w may also be expressed as the product of K_a for CH₃COOH and K_b for CH₃COO–. Thus, for a weak acid, HA, and its con- jugate weak base, A–,

This relationship between K_a and K_b simplifies the tabulation of acid and base dis- sociation constants. Acid dissociation constants for a variety of weak acids are listed in Appendix 3B. The corresponding values of K_b for their conjugate weak bases are determined using equation 6.14.