Chapter: Modern Analytical Chemistry: Equilibrium Chemistry
Le ChatelierŌĆÖs Principle
Le ChatelierŌĆÖs
Principle
The equilibrium position
for any reaction is defined
by a fixed equilibrium con- stant, not by a fixed combination of concentrations for the reactants and products. This is easily appreciated by examining the equilibrium constant
expression for the dissociation of acetic acid.
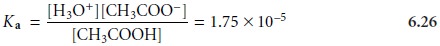
As a single
equation with three
variables, equation 6.26 does not have a unique so- lution for the concentrations of CH3COOH,
CH3COOŌĆō,
and H3O+. At constant
temperature, different solutions
of acetic acid may have different values for [H3O+], [CH3COOŌĆō] and [CH3COOH], but will always
have the same value of Ka.
If a solution of acetic acid
at equilibrium is disturbed by adding sodium
acetate, the [CH3COOŌĆō] increases, suggesting an apparent
increase in the value of Ka. Since Ka must remain constant, however, the concentration of all three
species in equa- tion 6.26 must change
in a fashion that restores Ka to its original value. In this
case, equilibrium is reestablished by the partial
reaction of CH3COOŌĆō
and H3O+ to pro- duce additional CH3COOH.
The observation that a system
at equilibrium responds
to a stress by reequili- brating in a manner that diminishes the stress, is formalized as Le Ch├ótelierŌĆÖs prin- ciple. One of the
most common stresses that we can
apply to a reaction at equilib-
rium is to change the concentration of a reactant
or product. We already have seen,
in the case of sodium
acetate and acetic
acid, that adding
a product to a reaction mixture at equilibrium converts a portion of the products to reactants. In this in- stance, we disturb the equilibrium by adding a product, and the stress
is diminished by partially reacting the excess
product. Adding acetic
acid has the opposite effect, partially converting the excess
acetic acid to acetate.
In our first
example, the stress
to the equilibrium was applied
directly. It is also
possible to apply a concentration stress indirectly. Consider, for example, the fol- lowing solubility equilibrium involving AgCl
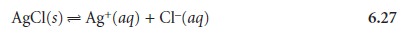
The effect on the solubility of AgCl of adding AgNO3 is obvious,* but what is the ef- fect
of adding a ligand that forms a stable, soluble
complex with Ag+? Ammonia, for example, reacts with Ag+ as follows
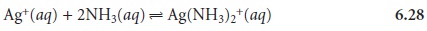
Adding ammonia decreases the concentration of Ag+ as the Ag(NH3)2+ complex forms. In turn, decreasing the concentration of Ag+ increases the solubility of AgCl
as reaction 6.27 reestablishes its equilibrium position. Adding together reactions 6.27 and
6.28 clarifies the
effect of ammonia
on the solubility of AgCl, by showing
that ammonia is a reactant.
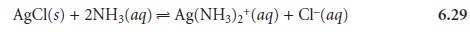

Increasing or decreasing the partial pressure
of a gas is the same as increasing
or decreasing its concentration.ŌĆĀ The effect on a reactionŌĆÖs equilibrium position can be analyzed
as described in the preceding example for aqueous
solutes. Since the concentration of a gas depends on its partial
pressure, and not on the total pressure of the system, adding
or removing an inert gas
has no effect
on the equilibrium po- sition of a gas-phase reaction.
Most reactions involve
reactants and products
that are dispersed in a solvent. If the amount of solvent is changed, either
by diluting or concentrating the
solu- tion, the concentrations of all reactants
and products either decrease or increase.
The effect of these changes
in concentration is not as intuitively obvious
as when the concentration of a single
reactant or product
is changed. As an example,
letŌĆÖs consider how dilution affects
the equilibrium position
for the formation of the aqueous silver-amine complex (reaction 6.28). The equilibrium constant for this reaction is
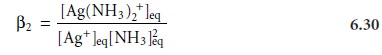
where the subscript ŌĆ£eqŌĆØ is included
for clarification. If a portion
of this solution is diluted with an equal volume
of water, each of the concentration terms
in equa- tion 6.30 is cut in half.
Thus, the reaction
quotient becomes
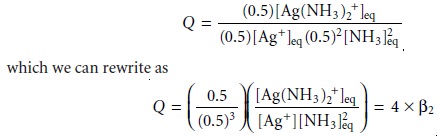
Since Q is greater
than ╬▓2, equilibrium must be reestablished by shifting the reac-
tion to the left, decreasing the concentration of Ag(NH3)2+. Furthermore, this new equilibrium position lies toward the side of the equilibrium reaction with the greatest number
of solutes (one
Ag+ ion and two molecules of NH3 versus
the sin- gle metalŌĆōligand complex). If the
solution of Ag(NH3)2+ is concentrated, by evapo- rating some of the
solvent, equilibrium is reestablished in the opposite direction. This is a general conclusion that can be applied to any reaction, whether gas-phase,
liquid-phase, or solid-phase. Increasing volume always
favors the direction pro- ducing the greatest
number of particles, and decreasing volume always favors the
direction producing the fewest particles. If the number
of particles is the same on
both sides of the equilibrium, then the equilibrium position is unaffected by a change in volume.
Related Topics