A More Complex Problem: The Common Ion Effect

A More Complex Problem: The Common Ion Effect

Calculating the solubility of Pb(IO₃)₂ in distilled water is a straightforward prob- lem since the dissolution of the solid is the only source of Pb2+ or IO₃–. How is the solubility of Pb(IO₃)₂ affected if we add Pb(IO₃)₂ to a solution of 0.10 M Pb(NO₃)₂? Before we set up and solve the problem algebraically, think about the chemistry occurring in this system, and decide whether the solubility of Pb(IO₃)₂ will increase, decrease, or remain the same. This is a good habit to develop. Knowing what answers are reasonable will help you spot errors in your calcula- tions and give you more confidence that your solution to a problem is correct.

We begin by setting up a table to help us keep track of the concentrations of P b2+ and IO₃– in this system.

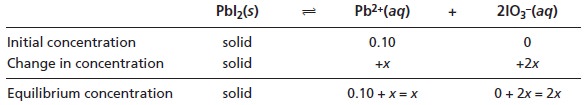
Substituting the equilibrium concentrations into the solubility product expression (equation 6.33)

(0.10 + x)(2x)2 = 2.5 x 10–13

and multiplying out the terms on the left leaves us with

4x3 + 0.40x2 = 2.5 x 10–13                                                            

This is a more difficult equation to solve than that for the solubility of Pb(IO₃)₂ in dis- tilled water, and its solution is not immediately obvious. A rigorous solution to equa- tion 6.34 can be found using available computer software packages and spreadsheets.

How might we solve equation 6.34 if we do not have access to a computer? One possibility is that we can apply our understanding of chemistry to simplify the algebra. From Le Châtelier’s principle, we expect that the large initial concentration of Pb2+ will significantly decrease the solubility of Pb(IO₃)₂. In this case we can reasonably expect the equilibrium concentration of Pb2+ to be very close to its initial concentration; thus, the following approximation for the equilibrium concentration of Pb2+ seems reasonable

[Pb2+] = 0.10 + x = 0.10 M

Substituting into equation 6.34

Before accepting this answer, we check to see if our approximation was reasonable. In this case the approximation 0.10 + x = 0.10 seems reasonable since the difference between the two values is negligible. The equilibrium concentrations of Pb2+ and IO₃–, therefore, are

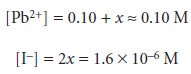
The solubility of Pb(IO₃)₂ is equal to the additional concentration of Pb2+ in solu- tion, or 7.9 x 10–7 mol/L. As expected, the solubility of Pb(IO₃)₂ decreases in the presence of a solution that already contains one of its ions. This is known as the common ion effect.

As outlined in the following example, the process of making and evaluating ap- proximations can be extended if the first approximation leads to an unacceptably large error.