Activity Effects

Activity Effects

Suppose you need to prepare a buffer with a pH of 9.36. Using the Henderson– Hasselbalch equation, you calculate the amounts of acetic acid and sodium acetate needed and prepare the buffer. When you measure the pH, however, you find that it is 9.25. If you have been careful in your calculations and measurements, what can account for the difference between the obtained and expected pHs? In this section, we will examine an important limitation to our use of equilibrium constants and learn how this limitation can be corrected.

Careful measurements of the solubility of AgIO₃ show that it increases in the presence of KNO₃, even though neither K+ or NO₃– participates in the solubility reaction. Clearly the equilibrium position for the reaction

AgIO₃(s)  < == === >  Ag+(aq)+ IO₃–(aq)

depends on the composition of the solution. When the solubility product for AgIO₃ is calculated using the equilibrium concentrations of Ag+ and IO₃–

K_sp = [Ag+][IO₃–]

its apparent value increases when an inert electrolyte such as KNO₃ is added.

Why should adding an inert electrolyte affect the equilibrium position of a chemical reaction? We can explain the effect of KNO₃ on the solubility of AgIO₃ by considering the reaction on a microscopic scale. The solution in which equilibrium is established contains a variety of cations and anions—K+, Ag+, H₃O+, NO₃–, IO₃– and OH–. Although the solution is homogeneous, on the average, there are more anions in regions near Ag+ ions, and more cations in regions near IO₃– ions. Thus, Ag+ and IO₃– are surrounded by charged ionic atmospheres that partially screen the ions from each other. The formation of AgIO₃ requires the disruption of the ionic atmospheres surrounding the Ag+ and IO₃– ions. Increasing the concentrations of ions in solution, by adding KNO₃, increases the size of these ionic atmospheres. Since more energy is now required to disrupt the ionic atmospheres, there is a decrease in the formation of AgIO₃, and an apparent increase in the equilibrium constant.

The ionic composition of a solution frequently is expressed by its ionic strength, μ

where c_i and z_i are the concentration and charge of the ith ion.

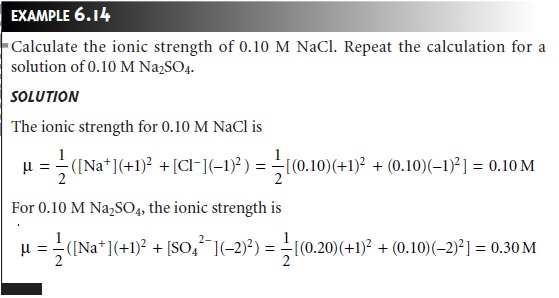
Note that the unit for ionic strength is molarity, but that the molar ionic strength need not match the molar concentration of the electrolyte. For a 1:1 electrolyte, such as NaCl, ionic strength and molar concentration are identical. The ionic strength of a 2:1 electrolyte, such as Na₂SO₄, is three times larger than the elec- trolyte’s molar concentration.

The true thermodynamic equilibrium constant is a function of activity rather than concentration. The activity of a species, a_A, is defined as the prod- uct of its molar concentration, [A], and a solution-dependent activity coeffi- cient, γ_A.

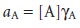
The true thermodynamic equilibrium constant, K_sp, for the solubility of AgIO₃, therefore, is

K_sp = (a_Ag+)(a_IO3 –) = [Ag+][IO₃^-](γ_Ag+)(γ_IO3–)

To accurately calculate the solubility of AgIO₃, we must know the activity coeffi- cients for Ag+ and IO₃ –.

For gases, pure solids, pure liquids, and nonionic solutes, activity coefficients are approximately unity under most reasonable experimental conditions. For reac- tions involving only these species, differences between activity and concentration are negligible. Activity coefficients for ionic solutes, however, depend on the ionic composition of the solution. It is possible, using the extended Debye–Hückel the- ory,* to calculate activity coefficients using equation 6.50

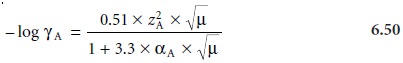
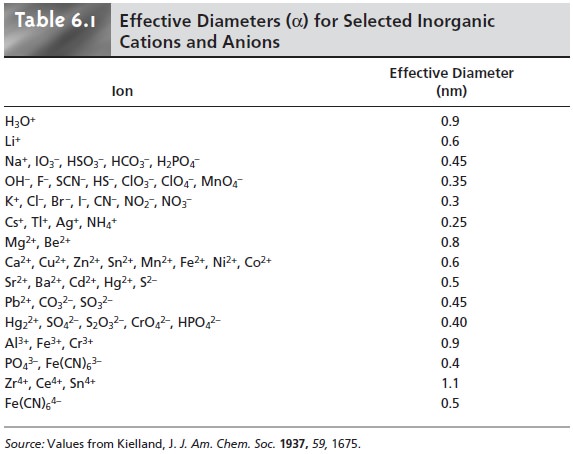
where Z_A is the charge of the ion, α_A is the effective diameter of the hydrated ion in nanometers (Table 6.1), μ is the solution’s ionic strength, and 0.51 and 3.3 are con- stants appropriate for aqueous solutions at 25 °C.

Several features of equation 6.50 deserve mention. First, as the ionic strength approaches zero, the activity coefficient approaches a value of one. Thus, in a solu- tion where the ionic strength is zero, an ion’s activity and concentration are identi- cal. We can take advantage of this fact to determine a reaction’s thermodynamic equilibrium constant. The equilibrium constant based on concentrations is mea- sured for several increasingly smaller ionic strengths and the results extrapolated back to zero ionic strength to give the thermodynamic equilibrium constant.

Second, activity coefficients are smaller, and thus activity effects are more important, for ions with higher charges and smaller effective diameters. Finally, the extended Debye–Hückel equation provides reasonable activity coefficients for ionic strengths of less than 0.1. Modifications to the extended Debye–Hückel equation, which extend the calculation of activity coefficients to higher ionic strength, have been proposed.

As this example shows, failing to correct for the effect of ionic strength can lead to significant differences between calculated and actual concentrations. Neverthe- less, it is not unusual to ignore activities and assume that the equilibrium constant is expressed in terms of concentrations. There is a practical reason for this—in an analysis one rarely knows the composition, much less the ionic strength of a sample solution. Equilibrium calculations are often used as a guide when developing an an- alytical method. Only by conducting the analysis and evaluating the results can we judge whether our theory matches reality.