Chapter: Modern Analytical Chemistry: Equilibrium Chemistry
Effect of Complexation on Solubility
Effect of Complexation on Solubility
The
solubility of
a precipitate can be improved by adding a ligand capable of forming a soluble
complex with one of the precipitate’s ions. For example, the solubility
of AgI increases in the presence of NH3 due to the formation of the soluble
Ag(NH3)2+ complex. As a final illustration of the systematic approach
to solving equilibrium problems, let us find the solubility of AgI in 0.10 M NH3.
We begin by writing the equilibria that we need to consider
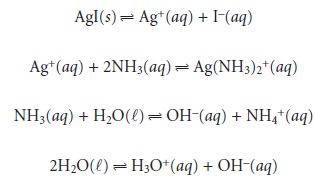
Counting
unknowns, we find that there are seven—[Ag+], [I–], [Ag(NH3)2+], [NH3], [NH4+], [OH–],
and [H3O+]. Four of the equations needed
to solve this problem are given by the equilibrium constant expressions

Three additional equations are needed. The first of these equations is a mass balance
for NH3.
CNH3 = [NH3] + [NH4+]+2 x [Ag(NH3)2+]
Note that in writing this
mass balance equation, the concentration of Ag(NH3)2+ must be multiplied by 2 since
two moles of NH3 occurs
per mole of Ag(NH3) +.
The second additional equation
is a mass balance on iodide and silver. Since AgI is the
only source of I– and Ag+, every iodide
in solution must
have an associated silver ion; thus
[I–]
= [Ag+]
+ [Ag(NH3) +]
Finally, the last equation is a charge balance equation
[Ag+] + [Ag(NH3)3+]2
+ [NH4+]+
[H3O+]=
[I–] +
[OH–]
Our problem looks
challenging, but several
assumptions greatly simplify
the al- gebra. First,
since the formation of the Ag(NH3) + complex is favorable, we will as- sume
that
[Ag+] << [Ag(NH3) +]
Second, since NH3 is a base, we will assume that
[H3O+] << [OH–]
[NH4+] << [NH3] + [Ag(NH3)
+]
Finally, since Ksp is significantly smaller
than β2, it seems likely
that the solubility of AgI is small and
[Ag(NH3) +] << [NH3]
Using these assumptions allows us to simplify several
equations. The mass
bal- ance for NH3 is now
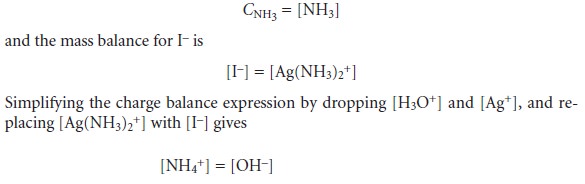
We continue by multiplying together the equations for Ksp and β2, giving

Substituting in the new mass balance equations for NH3
and I–
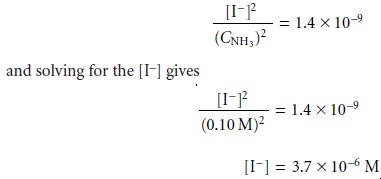
Before accepting this answer, we first check our assumptions.
Using the Ksp equation we calculate the [Ag+] to be
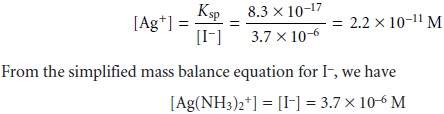
Our first assumption that the [Ag+] is significantly smaller than the [Ag(NH3) +], therefore, is reasonable. Furthermore, our third assumption that the [Ag(NH3)2+] is
significantly less than
the [NH3] also
is reasonable. Our
second assumption was

Although the [NH4+] is not significantly smaller than the combined concentrations of NH3 and Ag(NH3)2+, the error
is only about
1%. Since this is not an excessively large error, we will
accept this approximation as reasonable.
Since one mole of AgI produces one mole of I–, the solubility of AgI is the same as
the concentration of iodide, or 3.7 x 10–6 mol/L.
Related Topics