Ladder Diagrams for Complexation Equilibria

Ladder Diagrams for Complexation Equilibria

The same principles used in constructing and interpreting ladder diagrams for acid–base equilibria can be applied to equilibria involving metal–ligand com- plexes. For complexation reactions the ladder diagram’s scale is defined by the concentration of uncomplexed, or free ligand, pL. Using the formation of Cd(NH₃)2+ as an example

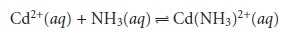
we can easily show that the dividing line between the predominance regions for Cd²⁺ and Cd(NH3)²⁺ is log(K₁).

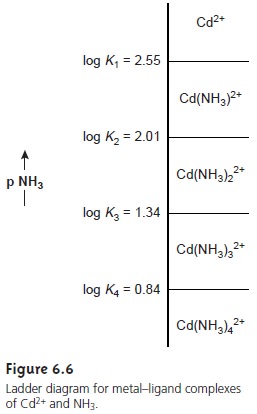
Since K₁ for Cd(NH3)²⁺ is 3.55 ´ 10², log(K₁) is 2.55. Thus, for a pNH₃ greater than 2.55 (concentrations of NH₃ less than 2.8 x 10^–3 M), Cd²⁺ is the predominate species. A complete ladder diagram for the metal–ligand complexes of Cd²⁺ and NH₃ is shown in Figure 6.6.

We can also construct ladder diagrams using cumulative formation constants in place of stepwise formation constants. The first three stepwise formation con- stants for the reaction of Zn2+ with NH₃

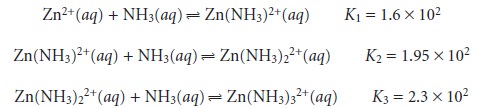
show that the formation of Zn(NH₃)₃2+ is more favorable than the formation of Zn(NH₃)2+ or Zn(NH₃)₂2+. The equilibrium, therefore, is best represented by the cumulative formation reaction

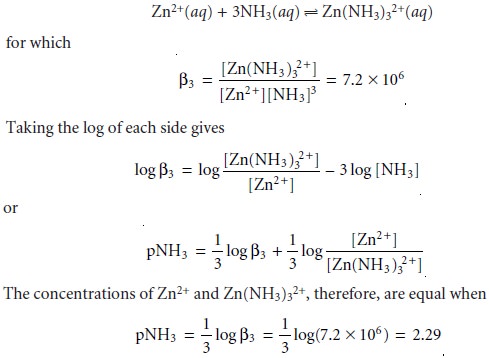
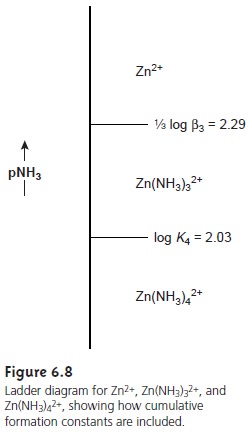
A complete ladder diagram for the Zn2+–NH₃ system is shown in Figure 6.8.