Equilibrium Constants for Complexation Reactions

Complexation Reactions

A more general definition of acids and bases was proposed by G. N. Lewis (1875–1946) in 1923. The Brønsted–Lowry definition of acids and bases focuses on an acid’s proton-donating ability and a base’s proton-accepting ability. Lewis the- ory, on the other hand, uses the breaking and forming of covalent bonds to describe acid–base characteristics. In this treatment, an acid is an electron pair acceptor, and a base is an electron pair donor. Although Lewis theory can be applied to the treat- ment of acid–base reactions, it is more useful for treating complexation reactions between metal ions and ligands.

The following reaction between the metal ion Cd2+ and the ligand NH₃ is typical of a complexation reaction.

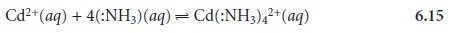
The product of this reaction is called a metal–ligand complex. In writing the equa- tion for this reaction, we have shown ammonia as :NH₃ to emphasize the pair of electrons it donates to Cd2+. In subsequent reactions we will omit this notation.

The formation of a metal–ligand complex is described by a formation con- stant, K_f. The complexation reaction between Cd2+ and NH₃, for example, has the following equilibrium constant

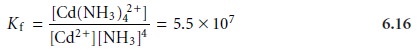
The reverse of reaction 6.15 is called a dissociation reaction and is characterized by a dissociation constant, K_d, which is the reciprocal of K_f.

Many complexation reactions occur in a stepwise fashion. For example, the re- action between Cd2+ and NH₃ involves four successive reactions

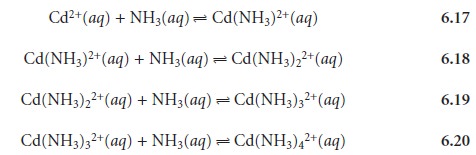
This creates a problem since it no longer is clear what reaction is described by a for- mation constant. To avoid ambiguity, formation constants are divided into two cat- egories. Stepwise formation constants, which are designated as K_i for the ith step, describe the successive addition of a ligand to the metal–ligand complex formed in the previous step. Thus, the equilibrium constants for reactions 6.17–6.20 are, re- spectively, K₁, K₂, K₃, and K₄. Overall, or cumulative formation constants, which are designated as β_i, describe the addition of i ligands to the free metal ion. The equilibrium constant expression given in equation 6.16, therefore, is correctly iden- tified as β₄, where

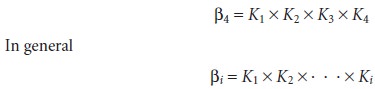
Stepwise and cumulative formation constants for selected metal–ligand complexes are given in Appendix 3C.

Equilibrium constants for complexation reactions involving solids are defined by combining appropriate K_sp and K_f expressions. For example, the solubility of AgCl increases in the presence of excess chloride as the result of the following com- plexation reaction

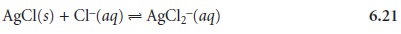
This reaction can be separated into three reactions for which equilibrium constants are known—the solubility of AgCl, described by its K_sp

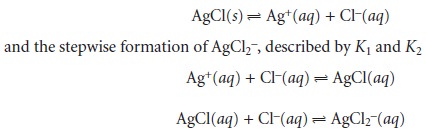
The equilibrium constant for reaction 6.21, therefore, is equal to K_sp x K₁ x K₂