Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Relation between Cp and Cv (Meyer's relation)
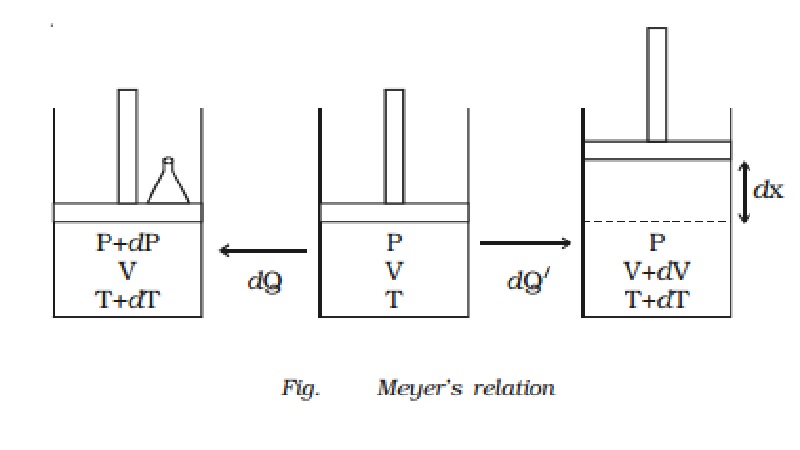
Relation between Cp and Cv (Meyer?s relation)
Let us consider
one mole of an ideal gas enclosed in a cylinder provided with a frictionless
piston of area A. Let P, V and T be the pressure, volume and absolute temperature of gas
respectively (Fig.).
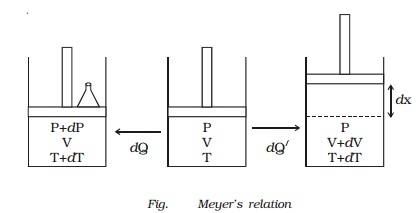
A quantity of heat dQ is supplied to the gas. To keep the
volume of the gas constant, a small weight is placed over the piston. The
pressure and the temperature of the gas increase to P + dP and T + dT
respectively. This heat energy dQ is
used to increase the internal energy dU of
the gas. But the gas does not do any work (dW
= 0).
∴ dQ = dU = 1 ? Cv ? dT ... (1)
The additional weight is now
removed from the piston. The piston now moves upwards through a distance dx, such that the pressure of the enclosed gas is equal to the atmospheric
pressure P. The temperature of the
gas decreases due to the expansion of the gas.
Now a quantity of heat dQ? is supplied to the gas till its temperature becomes T + dT. This heat energy is not only
used to increase the internal energy dU
of the gas but also to do external work dW
in moving the piston upwards.
dQ? = dU + dW
Since the expansion takes place
at constant pressure,
dQ ′ = CpdT
CpdT = CvdT + dW ????(2)
Work done, dW = force ? distance
= P ? A ? dx
dW = P dV (since A ? dx = dV, change in volume)
CpdT = CvdT + P dV ????(3)
The equation of state of an ideal
gas is
PV = RT
Differentiating both the sides
PdV = RdT ????(4)
Substituting equation (4) in (3),
CpdT = CvdT + RdT
Cp = Cv + R
Cp - Cv
= R
This equation is known as Meyer?s
relation
Related Topics