Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Indicator diagram (P-V diagram)

Indicator diagram (P-V diagram)
A curve showing variation of
volume of a substance taken along the X-axis and the variation of pressure
taken along Y-axis is called an indicator diagram or P-V diagram. The shape of
the indicator diagram shall depend on the nature of the thermodynamical process
the system undergoes.
Let us consider one mole of an
ideal gas enclosed in a cylinder fitted with a perfectly frictionless piston.
Let P1, V1 and T be the initial state of the gas. If dV
is an infinitesimally small increase in volume of the gas during which the
pressure P is assumed to be constant,
then small amount of workdone by the gas is dW
= PdV
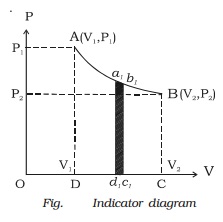
In the indicator diagram dW = area a1b1c1d1
The total workdone by the gas during expansion
from V1 to V2 is
W = ∫v1v2
PdV = Area ABCD, in the indicator
diagram.
Hence, in an indicator diagram
the area under the curve represents the work done (Fig.).
Isothermal process
When a gas undergoes expansion or
compression at constant temperature, the process is called isothermal process.
Let us consider a gas in a
cylinder provided with a frictionless piston. The cylinder and the piston are
made up of conducting material. If the piston is pushed down slowly, the heat
energy produced will be quickly transmitted to the surroundings. Hence, the
temperature remains constant but the pressure of the gas increases and its
volume decreases.
The equation for an isothermal
process is PV = constant.
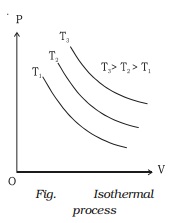
If a graph is drawn between P and V, keeping temperature constant, we get a curve called an
isothermal curve. Isotherms for three different temperatures T1, T2 and T3 are shown in the Fig.. The
curve moves away from the origin at higher temperatures.
During an isothermal change, the
specific heat capacity of the gas is infinite.
( i.e) C = ∆Q/m ∆T = infinity
(e.g) Melting of ice at its
melting point and vapourisation of water at its boiling point.
Workdone in an isothermal
expansion
Consider one mole of an ideal gas
enclosed in a cylinder with perfectly conducting walls and fitted with a
perfectly frictionless and conducting piston. Let P1, V1 and T be the initial pressure, volume and temperature of the gas. Let
the gas expand to a volume V2
when pressure reduces to P2,
at constant temperature T. At any
instant during expansion let the pressure of the gas be P. If A is the area of cross section of the piston, then force F = P ? A.
Let us assume that the pressure
of the gas remains constant during an infinitesimally small outward
displacement dx of the piston. Work
done
dW = Fdx = PAdx = PdV
Total work done by the gas in
expansion from initial volume V1
to final volume V2 is
W = ∫v1v2
PdV
We know, PV = RT, P =
RT/V
W = ∫v1v2 RT/V dV = RT ∫v1v2 1/V dV
W = RT [logeV]v1v2
W = RT [logeV2
- logeV1]
= RTloge (V2/V1)
This is the equation
for the workdone during an isothermal process.
Adiabatic process
In Greek, adiabatic means
?nothing passes through?. The process
in which pressure, volume and temperature
of a system change in such a manner that during the change no heat enters or
leaves the system is called adiabatic process. Thus in adiabatic process,
the total heat of the system remains
constant.
Let us consider a gas in a
perfectly thermally insulated cylinder fitted with a piston. If the gas is
compressed suddenly by moving the piston downward, heat is produced and hence
the temperature of the gas will increase. Such a process is adiabatic
compression.
If the gas is suddenly expanded
by moving the piston outward, energy required to drive the piston is drawn from
the internal energy of the gas, causing fall in temperature. This fall in
temperature is not compensated by drawing heat from the surroundings. This is
adiabatic expansion.
Both the compression and
expansion should be sudden, so that there is no time for the exchange of heat.
Hence, in an adiabatic process always there is change in temperature.
Expansion of steam in the
cylinder of a steam engine, expansion of hot gases in internal combustion
engine, bursting of a cycle tube or car tube, propagation of sound waves in a
gas are adiabatic processes.
The adiabatic relation between P and V for a gas, is
PVγ = k, a
constant ??..(1)
where γ = specific
heat capacity of the gas at constant pressure / specific heat capacity of the
gas at constant volume
From standard gas
equation,
PV = RT
P=RT/V
substituting the value
P in (1)
(RT/V ) Vγ
= constant
RT/ Vγ-1 =
constant
In an adiabatic
process Q =constant
∴ ∆Q = 0
∴ specific heat capacity C = ∆Q/m∆T
C=0
Work done in an adiabatic
expansion
Consider one mole of an ideal gas
enclosed in a cylinder with perfectly non conducting walls and fitted with a
perfectly frictionless, non conducting piston.
Let P1, V1 and
T1 be the initial pressure, volume and temperature of the gas.
If A is the area of cross section of
the piston, then force exerted by the gas on the piston is
F = P ? A, where P is
pressure of the gas at any instant during
expansion. If we assume that pressure of the gas remains constant during an
infinitesimally small outward displacement dx
of the piston,
then work done dW = F ? dx = P ? A dx dW = P dV
Total work done by the gas in
adiabatic expansion from volume V1 to
V2 is
W = ∫v1v2
PdV
But PVγ =
constant (k) for adiabatic process
where γ = Cp/Cv
W=∫v1v2kV-
γdV = k[V- γ /I- γ] v1v2
W = 1/(1- γ)[kV21-γ
? kV11-γ]
but, P2V2γ
= P1V1γ = k
??.(2)
Substituting the value
of k in (1)
W = 1/(1- γ)[P2V2
? P1V1]
If T2 is the final
temperature of the gas in adiabatic expansion, then
P1V1
= RT1,
P2V2 = RT2
Substituting in (3)
W = 1/(1- γ)[RT2
? RT2]
W= R/(1- γ)[ T2
?T2]
This is the equation
for the work done during adiabatic process.
Related Topics