Reflection at curved surfaces

Reflection at curved surfaces

In optics we are mainly concerned with curved mirrors which are the part of a hollow sphere (Fig. ). One surface of the mirror is silvered. Reflection takes place at the other surface. If the reflection takes place at the concave surface, (which is towards the centre of the sphere) it is called concave mirror. If the reflection takes place at the convex surface, (which is away from the centre of the sphere) it is called convex mirror. The laws of reflection at a plane mirror are equally true for spherical mirrors also.

The centre of the sphere, of which the mirror is a part is called  the centre of curvature (C).

The geometrical centre of the mirror is called its pole (P).

The line joining the pole of the mirror and its centre of curvature  is called the principal axis.

The distance between the pole and the centre of curvature of the spherical mirror is called the radius of curvature of the mirror and is also equal to the radius of the sphere of which the mirror forms a part.

When a parallel beam of light is incident on a spherical mirror, the point where the reflected rays converge (concave mirror) or appear to diverge from the point (convex mirror) on the principal axis is called the principal focus (F) of the mirror. The distance between the pole and the principal focus is called the focal length (f) of the mirror (Fig. ).

1.Images formed by a spherical mirror

The images produced by spherical mirrors may be either real or virtual and may be either larger or smaller than the object. The image can be located by graphical construction as shown in Fig.  by adopting any two of the following rules.

(i) A ray parallel to the principal axis after reflection by a concave mirror passes through the principal focus of the concave mirror and appear to come from the principal focus in a convex mirror.

(ii)                   A ray passing through the centre of curvature retraces its path after reflection.

(iii)A ray passing through the principal focus, after reflection is rendered parallel to the principal axis.

(iv)A ray striking the pole at an angle of incidence i is reflected at the same angle i to the axis.

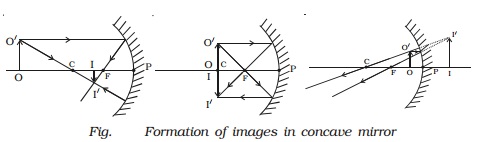
2 Image formed by a convex mirror

In a convex mirror irrespective of the position of the object, the image formed is always virtual, erect but diminished in size. The image

lies between the pole and the focus (Fig. ).

In general, real images are located in front of a mirror while virtual images behind the mirror.

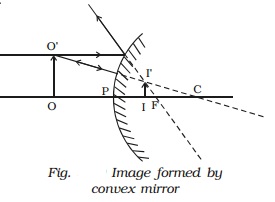
3 Cartesian sign convention

The following sign conventions are used.

(1)All distances are measured from the pole of the mirror (in the case of lens from the optic centre).

(2)The distances measured in the same direction as the incident light, are taken as positive.

(3)                  The distances measured in the direction opposite to the direction of incident light are taken as negative.

(4) Heights measured perpendicular to the principal axis, in the upward direction are taken as positive.

(5) Heights measured perpendicular to the principal axis, in the downward direction are taken as negative.

(6) The size of the object is always taken as positive, but image size is positive for erect image and negative for an inverted image.

(7)The magnification is positive for erect (and virtual) image, and negative for an inverted (and real) image.

4.Relation between u, v and f for spherical mirrors

A mathematical relation between object distance u, the image distance v and the focal length f of a spherical mirror is known as mirror formula.

(i) Concave mirror - real image

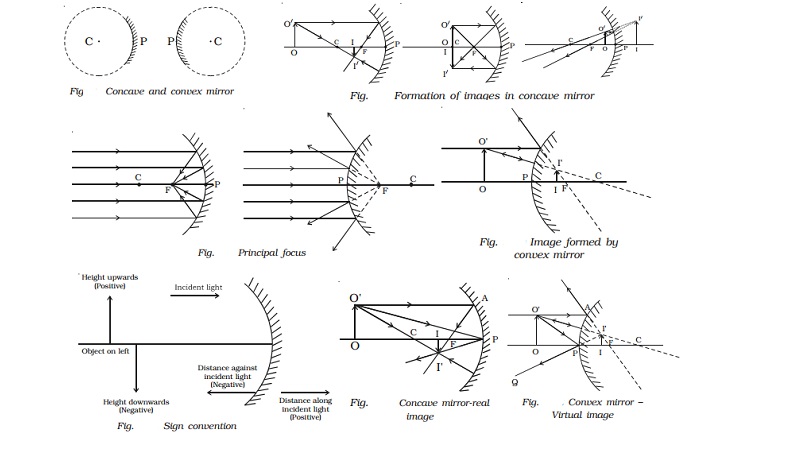
Let us consider an object OO′ on the principal axis of a concave mirror beyond C. The incident and the reflected rays are shown in the Fig . A ray O′A parallel to principal axis is incident on the concave mirror at A, close to P.  After reflections the ray passes through the focus F. Another ray O′C passing through centre of curvature C, falls normally on the mirror and reflected back along the same path. A third third ray 0?P incident at the pole P is reflected along PI′. The three reflected rays intersect at the point I′. Draw perpendicular I′I to the principal axis. II′ is the real, inverted image of the object OO?.

Right angled triangles, II?P and OO?P are similar.

II? / OO?  = PI/PO   ????..(1)

Right angled triangles II′F and APF are also similar (A is close to P ; hence AP is a vertical line)

II?/Ap = IF/PF  ???(2)

Comparing the equations (1) and (2)

PI/PO = IF/PF   ????(3)

But, IF = PI ? PF

Therefore equation (3) becomes

PI/PO = ( PI-PF ) / PF   ???..(4)

Using sign conventions, we have PO = ?u,

PI = -v and PF = -f

Substituting the values in the above equation, we get

[( -v/-u )]  - [(-v-(-f))(-f)]

Or

v/u = (v-f)/f=(v/f) ? 1

Dividing by v and rearranging, 1/u + 1/v = 1/f

This is called mirror equation. The same equation can be obtained for virtual image also.

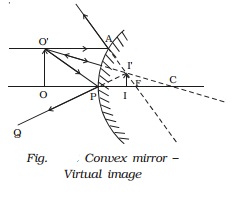
(ii) Convex mirror - virtual image

Let us consider an object OO′ anywhere on the principal axis of a convex mirror. The incident and the reflected rays are shown in the

Fig.. A ray O′A parallel to the principal axis incident on the convex mirror at A close to P. After reflection the ray appears to diverge from the focus F. Another ray O′C passing through centre of curvature C, falls normally on the mirror and is reflected back along the same path. A third ray O ′P incident at the pole P is reflected along PQ. The three reflected rays when produced appear to meet at the point I′. Draw perpendicular II′ to the principal axis. II′ is the virtual image of the object OO′.

Right angled triangles, II ′P and OO ′P are similar.

II?/OO? = PI/PO        ??(1)

Right angled triangles II ′F and APF are also similar (A is close to P; hence AP is a vertical line)

II? / AP = IF/PF

AP = OO ′. Therefore the above equation becomes,

II?/OO? = IF/PF   ??.(2)

Comparing the equations (1) and (2)

PI/PO = IF/PF   ????(3)

But, IF = PF ? PI. Therefore equation (3) becomes,

PI/PO = (PF-PI) / PF

Using sign conventions, we have PO = -u, PI = +v and PF = +f. Substituting the values in the above equation, we get

+v/-u = +f-(+v)   / +f

-v/u = (f-v) / f  = 1 ? (v/f)

This is called mirror equation for convex mirror producing virtual image.

5.Magnification

The linear or transverse magnification is defined as the ratio of the size of the image to that of the object.

∴Magnification =  size of the image / size of the object = h2/h1

where h₁ and h₂ represent the size of the object and image respectively.

From Fig.  it is known that II?/ OO?  =  PI/ PO

 Applying the sign conventions,

II′ = ?h2 (height of the image measured downwards)

OO ′ = +h1 (height of the object measured upwards)

PI = ?v (image distance against the incident light)

PO = ?u (object distance against the incident light)

Substituting the values in the above equation, we get

magnification m =( -h₂)/(+h₁) = -v/-u

For an erect image m is positive and for an inverted image m is negative. This can be checked by substituting values for convex mirror

also.

Using mirror formula, the equation for magnification can also be obtained as

m = h₂/h₁ = -v/u = (f-v)/f = f /(f-u)

This equation is valid for both convex and concave mirrors.