Pressure exerted by a gas

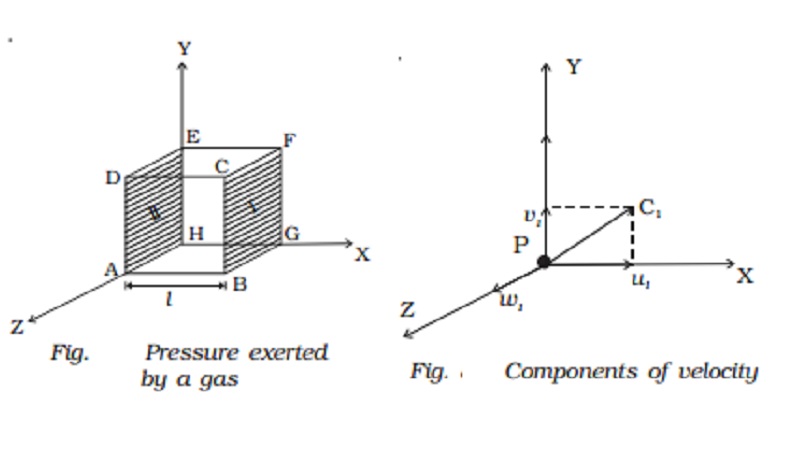
Pressure exerted by a gas

The molecules of a gas are in a state of random motion. They continuously collide against the walls of the container. During each collision, momentum is transfered to the walls of the container. The pressure exerted by the gas is due to the continuous  collision  of  the  molecules against the walls of the container. Due to this  continuous  collision,  the  walls experience a continuous force which is equal to the total momentum imparted to the walls per second. The force experienced per unit area of the walls of the container determines the pressure exerted by the gas.

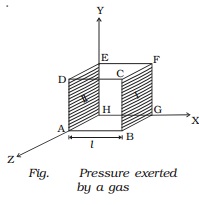
Consider a cubic container of side l containing n molecules of perfect gas moving with velocities C1, C2, C3 ... Cn (Fig.). A molecule moving with a  velocity C1, will have velocities u1, v1 and w1 as components along the x, y and z axes respectively. Similarly u2, v2 and w2 are the velocity components of the second molecule and so on. Let a molecule P (Fig.) having velocity C1 collide against the wall marked I (BCFG) perpendicular to the x-axis. Only the x-component of the velocity of the molecule is relevant for the wall I. Hence momentum of the molecule before collision is mu1 where m is the mass of the molecule. Since the collision is elastic, the molecule will rebound with the velocity u1 in the opposite direction. Hence momentum of the molecule after collision is ?mu1.

Change in the momentum of the molecule

= Final momentum - Initial momentum

= ?mu1 ? mu1 = ?2mu1

During each successive collision on face I the molecule must travel a distance 2l from face I to face II and back to face I.

Time taken between two successive collisions is = 2l/u₁

∴ Rate of change of momentum = Change in the momentum / Time taken

=  (-2mu₁) / (2l/u₁)

=  (-2mu₁²) / (2l)

=  -mu₁² / l

(i.e) Force exerted on the molecule =  -mu₁² / l

∴ According to Newton?s third law of motion, the force exerted by the molecule

= -(-mu₁² / l) =  mu₁² / l

Force exerted by all the n molecules is

F_x= mu₁² / l + mu₂² / l + ?? + mu_n² / l

Pressure exerted by the molecules

P_x=F_x/A

=1/l² ( [mu₁²]/l  + [mu₂²]/l + ?..+ [mu_n²]/l )

=m/l³(u₁² + u₂² + ?.+ u_n² )

Similarly, pressure exerted by the molecules along Y and Z axes are

P_y = m/l³(v₁²+ v₂²+ ???+ v_n²)

P_x = m/l³(w₁²+ w ₂²+ ???+ w _n²)

Since the gas exerts the same pressure on all the walls of the container

P_x = P_y = P_z = P

P = [P_x + P_y + P_z ]/3

P = 1/3 . m/l³. [C₁² + C₂² + .... + C_n² ]

where C₁² = (u₁² + v₁² + w₁² )

P = 1/3 . mn/V . C²

where C is called the root mean square (RMS) velocity, which is defined as the square root of the mean value of the squares of velocities of individual molecules.

(i.e.) C = root[ (C₁² + C₂² +?.+ C_n² ) / n ]

Relation between the pressure exerted by a gas and the mean

kinetic energy of translation per unit volume of the gas

Pressure exerted by unit volume of a gas, P = mnC² / 3

P = 1/3 .  ρC²  (∵ mn = mass per unit volume of the gas ; mn = ρ, density of the gas)

Mean kinetic energy of translation per unit volume of the gas

E =1/2 . ρC²

P/E = 2/3

P=2/3 . E

Average kinetic energy per molecule of the gas

Let us consider one mole of gas of mass M and volume V

P = 1/3 .  ρC²

P = 1/3 . M/V . C²

PV = 1/3 . M . C²

From gas equation

PV = RT

∴ RT =1/3 . M C²

3/2 . RT = ? . M C²

(i.e) Average kinetic energy of one mole of the gas is equal to 3/2 . RT

Since one mole of the gas contains N number of atoms where N is the Avogadro number

we have M = Nm

(1/2 ) . mNC² = 3/2 . RT

? mC² = 3/2 . R/N . T

=3/2 kT where k =R/N, is the Boltzmann constant Its value is 1.38 ? 10^-23 J K^-1

∴ Average kinetic energy per molecule of the gas is equal to 3/2 kT

Hence, it is clear that the temperature of a gas is the measure of the mean translational kinetic energy per molecule of the gas.