Pressure difference and pressure inside a liquid drop and a soap bubble

Pressure difference across a liquid surface

If the free surface of a liquid is plane, then the surface tension acts horizontally (Fig. a). It has no component perpendicular to the horizontal surface. As a result, there is no pressure difference between the liquid side and the vapour side.

If the surface of the liquid is concave (Fig. b), then the resultant  force R due to surface tension on a molecule on the surface act vertically upwards. To balance this, an excess of pressure acting downward on the concave side is necessary. On the other hand if the surface is convex (Fig. c), the resultant R acts downward and there must be an excess of pressure on the concave side acting in the upward direction.

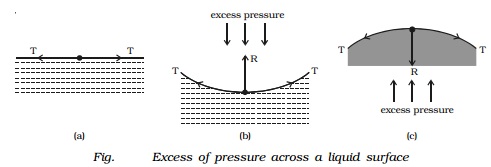
Thus, there is always an excess of pressure on the concave side of a curved liquid surface over the pressure on its convex side due to surface tension.

Excess pressure inside a liquid drop

Consider a liquid drop of radius r. The molecules on the surface of the drop experience a resultant force acting inwards due to surface tension. Therefore, the pressure inside the drop must be greater than the pressure outside it. The excess of pressure P inside the drop provides a force acting outwards perpendicular to the surface, to balance the resultant force due to surface tension. Imagine the drop to be divided into two equal halves. Considering the equilibrium of the upper hemisphere of the drop, the upward force on the plane face ABCD due to excess pressure P is P π r ² (Fig.).

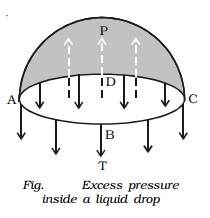
If T is the surface tension of the liquid, the force due to surface tension acting downward along the circumference of the circle ABCD is T 2πr.

At equilibrium, Pπr ² = T 2πr

P = 2T/r

Excess pressure inside a soap bubble

A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. Therefore the force due to surface tension = 2 × 2πrT

∴ At equilibrium, P πr 2 = 2 × 2πrT

P=4T/r

Thus the excess of pressure inside a drop is inversely proportional to its radius i.e P α 1/r. As P α 1/r. the pressure needed to form a very small bubble is high. This explains why one needs to blow hard to start a balloon growing. Once the balloon has grown, less air pressure is needed to make it expand more.