Oscillations of a simple pendulum

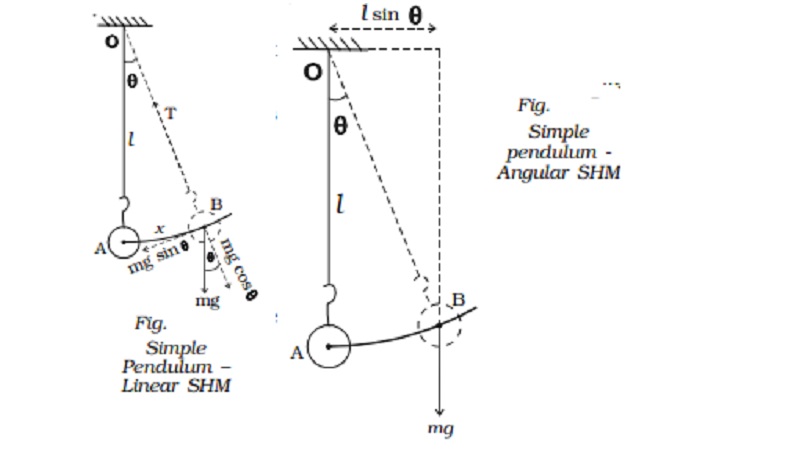
Oscillations of a simple pendulum

 A simple pendulum consists of massless and inelastic thread whose one end is fixed to a rigid support and a small bob of mass m is suspended from the other end of the thread. Let l be the length of the pendulum. When the bob is slightly displaced and released, it oscillates about its equilibrium position. Fig. shows the displaced position of the pendulum.

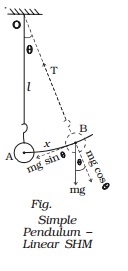
Suppose the thread makes an angle θ with the vertical. The distance of the bob from the equilibrium position A is AB. At B, the weight mg acts vertically downwards. This force is resolved into two components.

(i)                The component mg cos θ is balanced by the tension in the thread acting along the length towards the fixed point O.

(ii)             mg sin θ which is unbalanced, acts perpendicular to the length of thread. This force tends to restore the bob to the mean position. If the amplitude of oscillation is small, then the path of the bob is a straight line

∴ F = −mg sin θ ...(1)

If the angular displacement is small sin θ ≈ θ

∴ F = −mg θ  ???.(2)

But θ = x/l

∴ F = − mg (x/l)

Comparing this equation with Newton?s second law, F = ma we get, acceleration a = -gx/l ?(3)

(negative sign indicates that the direction of acceleration is opposite to the displacement) Hence the motion of simple pendulum is SHM.

We know that a = −ω²x

Comparing this with (3)

ω² = g/l  or ω =rt(g/l) ----(4)

Time period T = 2 π/ ω

T = 2 π rt(l/g)

∴ frequency n = 1/2 πrt(g/l)   ?..(6)

Laws of pendulum

From the expression for the time period of oscilations of a pendulum the following laws are enunciated.

         ( i) The law of length

The period of a simple pendulum varies directly as the square root of the length of the pendulum. (i.e) T α l

(ii)The law of acceleration

The period of a simple pendulum varies inversely as the square root of the acceleration due to gravity.

(i.e) T α 1 g

(iii) The law of mass

 The time period of a simple pendulum is independent of the mass and material of the bob.

(iv)The law of amplitude

The period of a simple pendulum is independent of the amplitude provided the amplitude is small.

Note : The length of a seconds pendulum is 0.99 m whose period is two seconds.

2 = 2π.rt(l/g)

l=  9.81x 4 / 4 π²=0.99 m

Oscillations of simple pendulum can also be regarded as a case of angular SHM.

Let θ be the angular displacement of the bob B at an instant of time. The bob makes rotation about the horizontal line which is perpendicular to the plane of motion as shown in Fig..

Restoring torque about O is τ = − mg l sin θ

τ = −m g l θ [ ∵ θ is sm all] ...(1)

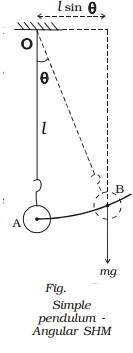
Moment of inertia about the axis = m l ² ...(2)

If the amplitude is small, motion of the bob is angular simple harmonic. Therefore angular acceleration of the system about the axis of rotation is

α = r/l = -mgl θ / ml²

α = - (g/l) θ   ?.(3)

We know that α = −ω ² θ        ??.(4)

Comparing (3) and (4)

−ω ²θ = -(g/l) θ

angular frequency ω = rt(g/l)

Time period T = = 2π / ω = 2π .rt(l/g)

Frequency n = 1 / 2 π . rt(g/l)