Oscillation of liquid column in a U - tube

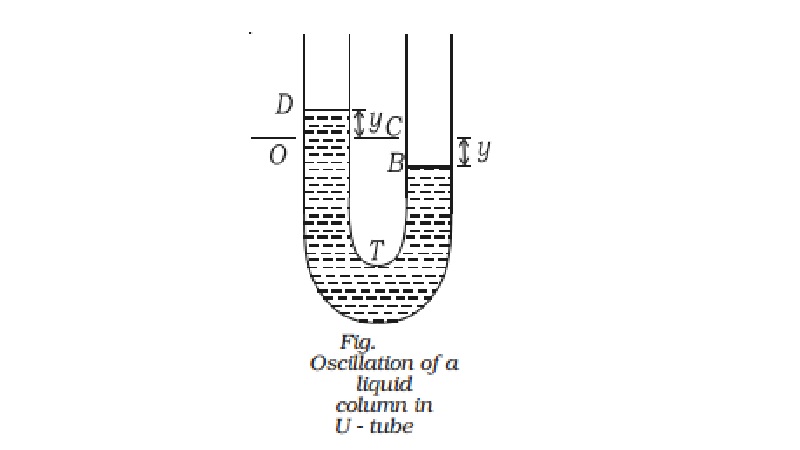
Oscillation of liquid column in a U - tube

Consider a non viscous liquid column of length l of uniform cross-sectional area A (Fig.). Initially the level of liquid in the limbs is the same. If the liquid on one side of the tube is depressed by blowing gently the levels of the liquid oscillates for a short time about their initial positions O and C, before coming to rest. If the liquid in one of the limbs is depressed by y , there will be a difference of 2 y in the liquid levels in the two limbs. At some instant, suppose the level of the liquid on the left side of the tube is at D, at a height y above its original position O, the level B of the liquid on the other side is then at a depth y below its original position C. So the excess pressure P on the liquid due to the restoring force is excess height ? density ? g

(i.e) pressure = 2 y ρ g

∴ Force on the liquid = pressure ? area of the cross-section of the tube

 = ? 2 y ρ g ? A      ???.(1)

The negative sign indicates that the force towards O is opposite to the displacement measured from O at that instant.

The mass of the liquid column of length l is volume ? density

(i.e) m = l A ρ

∴ F = l A ρ a .... (2)

From equations (1) and (2)

l A ρ a = - 2 y A ρ g

∴ a = ? 2g /l . y

We know that a = ?ω² y

(i.e) a = ? 2 g/ l . y= ?ω² y

where ω = rt(2g/l)

Here, the acceleration is proportional to the displacement, so the motion is simple harmonic and the period T is

T=[ 2π / ω ] -  [2π rt(l/2g)]