Newton's law of gravitation

Newton's law of gravitation

The motion of the planets, the moon and the Sun was the interesting subject among the students of Trinity college at Cambridge in England.

Newton  was  also  one  among  these students. In 1665, the college was closed for an indefinite period due to plague. Newton, who was        then   23      years old, went     home to Lincolnshire. He continued to think about the motion of planets and the moon. One day Newton sat under an apple tree and had tea with his friends. He saw an apple falling to ground. This incident made him to think about falling bodies. 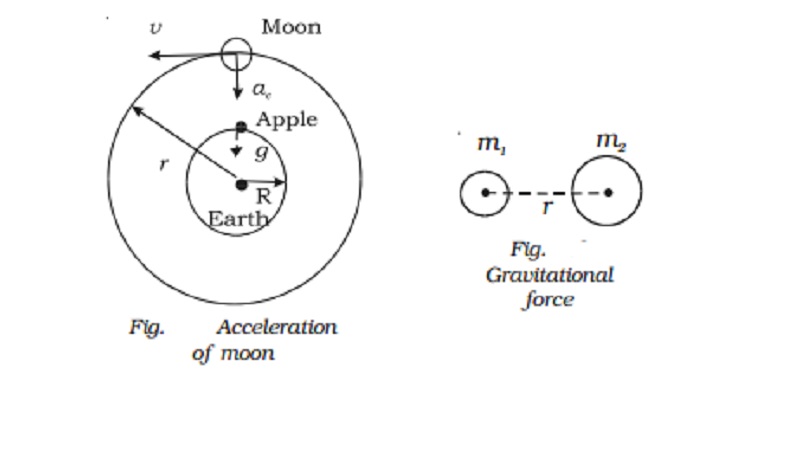He concluded that the same force of gravitation which attracts the apple to the Earth might also be responsible for attracting the moon and keeping it in its orbit. The centripetal acceleration of the moon in its orbit and the downward acceleration of a body falling on the Earth might have the same origin. Newton calculated the centripetal acceleration by assuming moon's orbit (Fig.) to be circular.

Acceleration due to gravity on the Earth's surface, g = 9.8 m s^-2

Centripetal acceleration on the moon, a^c = v²/r

where r is the radius of the orbit of the moon (3.84 × 10⁸ m) and v is the speed of the moon.

Time period of revolution of the moon around the Earth,

T = 27.3 days.

The speed of the moon in its orbit, v = 2πr /T

v = = 1.02 × 10³ m s⁻¹

Centripetal acceleration, a_c  = v²/r = 2.7 × 10⁻³ m s⁻²

Newton assumed that both the moon and the apple are accelerated towards the centre of the Earth. But their motions differ, because, the moon has a tangential velocity whereas the apple does not have.

Newton found that a_c was less than g and hence concluded that force produced due to gravitational attraction of the Earth decreases with increase in distance from the centre of the Earth. He assumed that this acceleration and therefore force was inversely proportional to the square of the distance from the centre of the Earth. He had found that the value of a_c was about 1/3600 of the value of g, since the radius of the lunar orbit r is nearly 60 times the radius of the Earth R.

The value of a_c was calculated as follows :

A_c/g = (1/r²)  / (1/R²) = 1/3600

A_c =  9.8/3600 = 2.7 × 10⁻³ m s⁻²

Newton suggested that gravitational force might vary inversely as the square of the distance between the bodies. He realised that this force of attraction was a case of universal attraction between any two bodies present anywhere in the universe and proposed universal gravitational law.

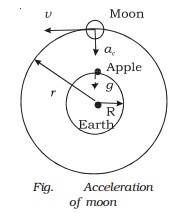
The law states that every particle of matter in the universe attracts every other particle with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Consider two bodies of masses m₁ and m₂ with their centres separated by a distance r. The gravitational force between them is

F  α  m₁m₂

F α 1/r²

F = G m₁m_{2 /} r²

where G is the universal gravitational constant.

If m₁ = m₂ = 1 kg and r = 1 m, then F = G.

_{Hence, the Gravitational constant 'G' is  numerically equal to the  gravitational  force of attraction        between   two  bodies of mass 1  kg  each  separated by a  distance of  1  m.  The  value of G  is} 6.67 × 10⁻¹¹ N m² kg⁻² and its dimensional formula is M⁻¹ L³ T⁻²

Special features of the law

          The gravitational force between two bodies is an action and reaction pair.

              The gravitational force is very small in the case of lighter bodies. It is appreciable in the case of massive bodies. The gravitational force between the Sun and the Earth is of the order of 10²⁷ N.