Ladder Diagrams for Acid–Base Equilibria

Ladder Diagrams for Acid–Base Equilibria

To see how a ladder diagram is constructed, we will use the acid–base equilibrium between HF and F–

Finally, replacing the negative log terms with p-functions and rearranging leaves us with

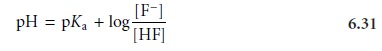
Examining equation 6.31 tells us a great deal about the relationship between pH and the relative amounts of F– and HF at equilibrium. If the concentrations of F– and HF are equal, then equation 6.31 reduces to

pH= pK_a,HF = –log(K_a,HF) = –log(6.8 x 10–4) = 3.17

For concentrations of F– greater than that of HF, the log term in equation 6.31 is positive and

pH> pK_a,HF or pH > 3.17

This is a reasonable result since we expect the concentration of hydrofluoric acid’s conjugate base, F–, to increase as the pH increases. Similar reasoning shows that the concentration of HF exceeds that of F– when

pH < pK_a,HF or pH < 3.17

Now we are ready to construct the ladder diagram for HF (Figure 6.4). The ladder diagram consists of a vertical scale of pH values oriented so that smaller (more acidic) pH levels are at the bottom and larger (more basic) pH levels are at the top. A horizontal line is drawn at a pH equal to pK_a,HF. This line, or step, separates the solution into regions where each of the two conjugate forms of HF predominate.

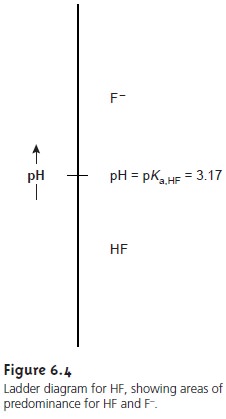
By referring to the ladder diagram, we see that at a pH of 2.5 hydrofluoric acid will exist predominately as HF. If we add sufficient base to the solution such that the pH increases to 4.5, the predominate form be- comes F–.

Figure 6.5 shows a second ladder diagram containing information about  HF/F– and NH₄ +/NH₃ .  From this ladder diagram we see that if the pH is less than 3.17, the predominate species are HF and NH₄+. For pH’s between 3.17 and 9.24 the predominate species are F– and NH₄+, whereas above a pH of 9.24 the predominate species are F– and NH₃.

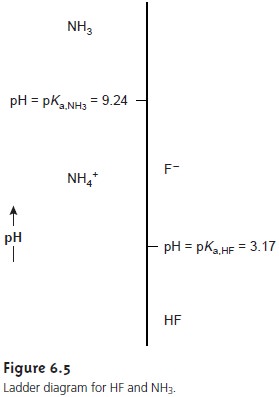
Ladder diagrams are particularly useful for evaluating the reactivity of acids and bases. An acid and a base cannot coexist if their respective areas of predominance do not overlap. If we mix together solutions of NH₃ and HF, the reaction

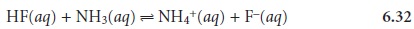
 occurs because the predominance areas for HF and NH₃ do not overlap. Be- fore continuing, let us show that this conclusion is reasonable by calculating the equilibrium constant for reaction 6.32. To do so we need the following three reactions and their equilibrium constants.

Since the equilibrium constant is significantly greater than 1, the reaction’s equilib- rium position lies far to the right. This conclusion is general and applies to all lad- der diagrams. The following example shows how we can use the ladder diagram in Figure 6.5 to evaluate the composition of any solution prepared by mixing together solutions of HF and NH₃.

If the areas of predominance for an acid and a base overlap each other, then practically no reaction occurs. For example, if we mix together solutions of NaF and NH₄Cl, we expect that there will be no significant change in the moles of F– and NH₄+. Furthermore, the pH of the mixture must be between 3.17 and 9.24. Because F– and NH₄+ can coexist over a range of pHs we cannot be more specific in estimat- ing the solution’s pH.

The ladder diagram for HF/F– also can be used to evaluate the effect of pH on other equilibria that include either HF or F–. For example, the solubility of CaF₂

CaF₂(s)  < = = = >  tCa2+(aq)+ 2F–(aq)

is affected by pH because F– is a weak base. Using Le Châtelier’s principle, if F– is converted to HF, the solubility of CaF₂ will increase. To minimize the solubility of CaF₂ we want to control the solution’s pH so that F– is the predominate species. From the ladder diagram we see that maintaining a pH of more than 3.17 ensures that solubility losses are minimal.