Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Gravitational field: potential difference and potential energy
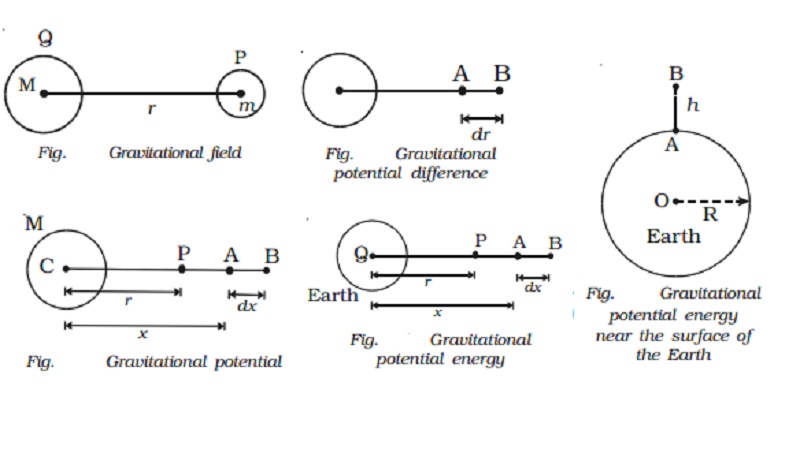
Gravitational field
Two masses
separated by a distance exert gravitational forces on one another. This is
called action at-a-distance. They interact even though they are not in contact.
This interaction can also be explained with the field concept. A particle or a body placed at a point
modifies a space around it which is
called gravitational field. When another particle is brought in this field, it experiences gravitational force of
attraction.
The gravitational field is defined as the space around a mass in
which it can exert gravitational force on other mas.
Gravitational field intensity
Gravitational field intensity or strength at a point is defined
as the force experienced by a unit mass placed at that point. It is denoted by E.
It is a vector quantity. Its unit
is N kg-1.
Consider a body of mass M placed at a point Q and another body of mass m
placed at P at a distance r from Q.

The mass M develops a field E at P and this field exerts a force
F = mE.
The gravitational force of
attraction between the masses m and M
is F = GMm/r2
The gravitational field intensity
at P is E = F/m
E = GM/r2
Gravitational field intensity is
the measure of gravitational field.
Gravitational potential difference
Gravitational potential
difference between two points is defined as the amount of work done in moving
unit mass from one point to another point against the gravitational force of
attraction.
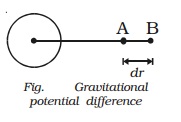
Consider two points A and B separated by a distance
dr in the gravitational field.
The work done in moving unit mass
from A to B is dv = WA → B
Gravitational potential
difference dv = − E dr
Here negative sign indicates that
work is done against the gravitational field.
Gravitational potential
Gravitational potential at a
point is defined as the amount of work done in moving unit mass from the point
to infinity against the gravitational field. It is a scalar quantity. Its unit
is N m kg-1.
Expression for gravitational
potential at a point
Consider a body of mass M at the point C. Let P be a point at a
distance r from C. To calculate the gravitational potential at P consider two points A
and B. The point A, where the unit mass is placed
is at a distance x from C.
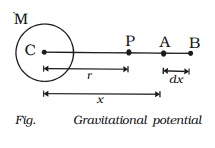
The gravitational field at A is E
= GM/x2
The work done in moving the unit
mass from A to B through a small distance dx is dw = dv = −E.dx
Negative sign indicates that work
is done against the gravitational field.
dv = − ( GM/x2 ) dx
The work done in moving the unit
mass from the point P to infinity is
∫dv = - ∫(GM/x2) dx
v= - GM/r
The gravitational potential is
negative, since the work is done against the field. (i.e) the gravitational
force is always attractive.
Gravitational potential energy
Consider a body of mass m placed
at P at a distance r from the centre of the Earth. Let the mass of the Earth be
M.
When the mass m is at A at a
distance x from Q, the gravitational force of attraction on it due to mass M is
given by F = GMm / x2
The work done in moving the mass
m through a small distance dx from A to B along the line joining the
two centres of masses m and M is
dw = -F.dx.
Negative sign indicates that work
is done against the gravitational field.
dw = - GMm / x2 dx
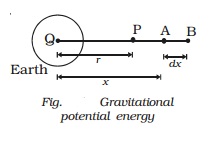
The gravitational potential
energy of a mass m at a distance r from another mass M is defined as the amount
of work done in moving the mass m from a distance r to infinity.
The total work done in moving the
mass m from a distance r to infinity is
*U = GMm/r
Gravitational potential energy is
zero at infinity and decreases as the distance decreases. This is due to the
fact that the gravitational force exerted on the body by the Earth is
attractive. Hence the gravitational potential energy U is negative.
Gravitational potential energy near the surface of the Earth
Let the mass of the Earth be M
and its radius be R. Consider a point A on the surface of the Earth and another
point B at a height h above the surface of the Earth. The work done in moving
the mass m from A to B is U = UB − UA
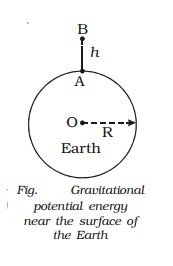
U = GMmh / R(R+h)
If the body is near the surface
of the Earth, h is very small when compared with R. Hence (R+h) could be taken
as R.
U = GMmh / R2
U = mgh
Related Topics