Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Experimental verification of Newton's law of cooling
Newton s law of cooling
Newton s law of cooling states
that the rate of cooling of a body is
directly proportional to the temperature
difference between the body and the surroundings.
The law holds good only for a
small difference of temperature. Loss of heat by radiation depends on the
nature of the surface and the area of the exposed surface.
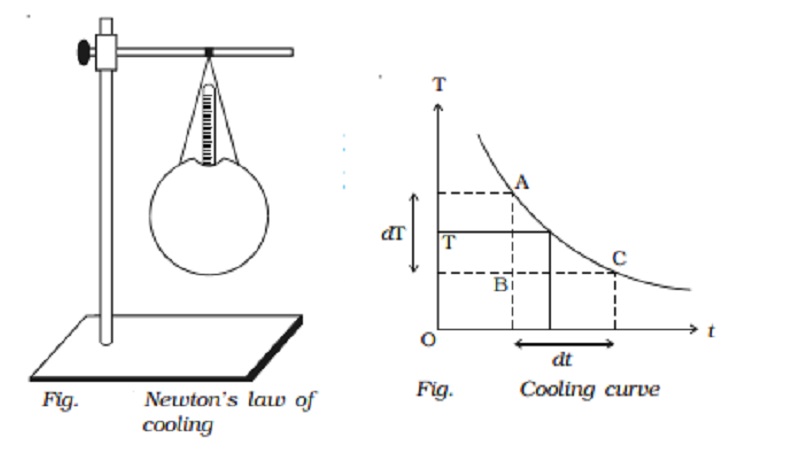
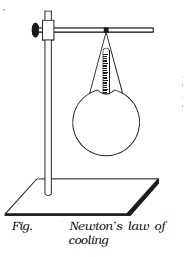
Experimental verification of Newton s law of cooling
Let us consider a spherical
calorimeter of mass m whose outer surface is blackened. It is filled with hot
water of mass m1. The calorimeter with a thermometer is suspended
from a stand (Fig.).
The calorimeter and the hot water
radiate heat energy to the surroundings. Using a stop clock, the temperature is
noted for every 30 seconds interval of time till the temperature falls by about
20o C. The readings are entered in a tabular column.
If the temperature of the
calorimeter and the water falls from T1 to T2 in t
seconds, the quantity of heat energy lost by radiation
Q = (ms + m1s1)
(T1 ? T2), where s
is the specific heat capacity of the material of the calorimeter and s1 is the
specific heat capacity of water.
Rate of cooling = Heat energy
lost / time taken
Q / t = (ms + m1s1
)(T1 ? T2 ) / t
If the room temperature is To,
the average excess temperature of the calorimeter over that of the surroundings
is ( [ (T1 + T2) /
2 ] - T0)
According to Newton?s Law of
cooling, Q/t α ( [ (T1 + T2) / 2 ] - T0)
(ms + m1s1
)(T1 ? T2 )
/ t[((T1+T2)/2)
? T0] = constant
The time for every 4o
fall in temperature is noted. The last column in the tabular column is found to
be the same. This proves Newton?s Law of cooling.
Table Index : Newton?s law of
cooling
1. Temperature range
2. Time t for every 4o
fall of temperature
3. Average excess of
temperature ( [ (T1 + T2)
/ 2 ] - T0)
4. ( [ (T1 + T2)
/ 2 ] - T0)t

A cooling curve is drawn by
taking time along X-axis and temperature along Y-axis (Fig.).
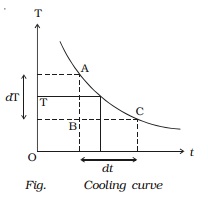
From the cooling curve, the rate
of fall of temperature at T is dT/dt = AB/BC
The rate of cooling dT/dt is
found to be directly proportional to (T - To). Hence Newton?s law of
cooling is verified.
Related Topics