Experimental determination of surface tension of water by capillary rise method

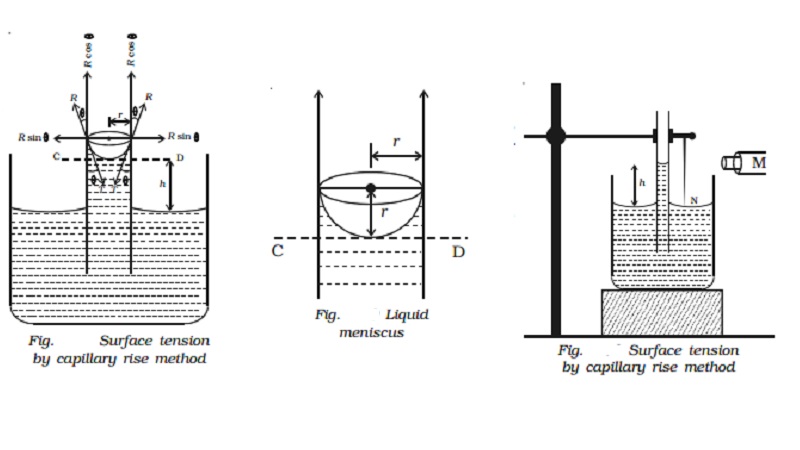
Surface tension by capillary rise method

Let us consider a capillary tube of uniform bore dipped vertically in a beaker containing water. Due to surface tension, water rises to a height h in the capillary tube as shown in Fig.. The surface tension T of the water acts inwards and the reaction of the tube R outwards. R is equal to T in magnitude but opposite in direction. This reaction R can be resolved into two rectangular components.

(i)                   Horizontal component R sin θ acting radially outwards

(ii)                 Vertical component R cos θ acting upwards.

The horizontal component acting all along the circumference of the tube cancel each other whereas the vertical component balances the weight of water column in the tube.

Total upward force = R cos θ × circumference of the tube

(i.e) F = 2πr R cos θ or F = 2πr T cos θ          ……………(1)

This upward force is responsible for the capillary rise. As the water column is in equilibrium, this force acting upwards is equal to weight of the water column acting downwards.

F = W   ………(2)

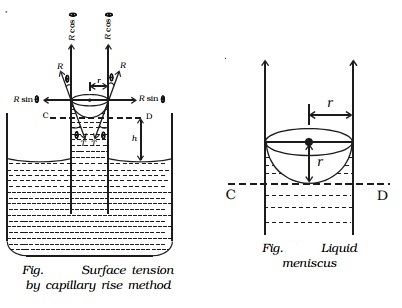
Now, volume of water in the tube is assumed to be made up of (i) a cylindrical water column of height h and (ii) water in the meniscus above the plane CD.

Volume of cylindrical water column = πr²h

Volume of water in the meniscus = (Volume of cylinder of height r and radius r) - (Volume of hemisphere)

Volume of water in the meniscus = (πr² × r) - (2/3 π r³)  = 1/3 πr³

Total volume of water in the tube = πr² (h+ r/3)

If ρ is the density of water, then weight of water in the tube is W = πr² (h+ r/3) ρg   ………….(3)

Substituting (1) and (3) in (2),

T = (h+r/3)r ρg    /  2cos θ

Since r is very small, r/3 can be neglected compared to h.

T = hr ρ g / 2 cos θ

For water, θ is small, therefore cos θ = 1

 T = hr ρ g / 2

Experimental determination of surface tension of water by capillary rise method

A clean capillary tube of uniform bore is fixed vertically with its lower end dipping into water taken in a beaker. A needle N is also fixed with the capillary tube as shown in the Fig.. The tube is raised or lowered until the tip of the needle just touches the water surface. A travelling microscope M is focussed on the meniscus of the water in the capillary tube. The reading R₁ corresponding to the lower meniscus is noted. The microscope is lowered and focused on the tip of the needle and the corresponding reading is taken as R₂. The difference between R₁ and R₂ gives the capillary rise h.

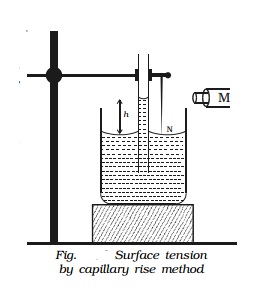
The radius of the capillary tube is determined using the travelling microscope. If ρ is the density of water then the surface tension of water is given by T = hrρg /2 where g is the acceleration due to gravity.