Equilibrium Constants for Oxidation–Reduction Reactions

Oxidation–Reduction Reactions

In a complexation reaction, a Lewis base donates a pair of electrons to a Lewis acid. In an oxidation–reduction reaction, also known as a redox reaction, electrons are not shared, but are transferred from one reactant to another. As a result of this elec- tron transfer, some of the elements involved in the reaction undergo a change in ox- idation state. Those species experiencing an increase in their oxidation state are oxi- dized, while those experiencing a decrease in their oxidation state are reduced. For example, in the following redox reaction between Fe3+ and oxalic acid, H₂C₂O₄, iron is reduced since its oxidation state changes from +3 to +2.

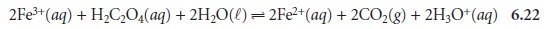
Oxalic acid, on the other hand, is oxidized since the oxidation state for carbon in- creases from +3 in H₂C₂O₄ to +4 in CO₂.

Redox reactions, such as that shown in equation 6.22, can be divided into sepa- rate half-reactions that individually describe the oxidation and the reduction processes.

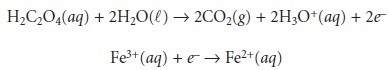
It is important to remember, however, that oxidation and reduction reactions al- ways occur in pairs.* This relationship is formalized by the convention of calling the species being oxidized a reducing agent, because it provides the electrons for the re- duction half-reaction. Conversely, the species being reduced is called an oxidizing agent. Thus, in reaction 6.22, Fe3+ is the oxidizing agent and H₂C₂O₄ is the reducing agent.

The products of a redox reaction also have redox properties. For example, the Fe2+ in reaction 6.22 can be oxidized to Fe3+, while CO₂ can be reduced to H₂C₂O₄. Borrowing some terminology from acid–base chemistry, we call Fe2+ the conjugate reducing agent of the oxidizing agent Fe3+ and CO₂ the conjugate oxidizing agent of the reducing agent H₂C₂O_4.

Unlike the reactions that we have already considered, the equilibrium position of a redox reaction is rarely expressed by an equilibrium constant. Since redox reac- tions involve the transfer of electrons from a reducing agent to an oxidizing agent, it is convenient to consider the thermodynamics of the reaction in terms of the electron.

The free energy, ∆G_, associated with moving a charge, Q, under a potential, E, is given by

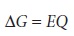
Charge is proportional to the number of electrons that must be moved. For a reac- tion in which one mole of reactant is oxidized or reduced, the charge, in coulombs, is

Q = nF

where n is the number of moles of electrons per mole of reactant, and F is Faraday’s constant (96,485 C . mol–1). The change in free energy (in joules per mole; J/mol) for a redox reaction, therefore, is

∆G = –nFE       6.23

where ∆G has units of joules per mole. The appearance of a minus sign in equation 6.23 is due to a difference in the conventions for assigning the favored direction for reactions. In thermodynamics, reactions are favored when ∆G is negative, and redox reactions are favored when E is positive.

The relationship between electrochemical potential and the concentrations of reactants and products can be determined by substituting equation 6.23 into equation 6.3

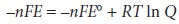
where E° is the electrochemical potential under standard-state conditions. Dividing through by –nF leads to the well-known Nernst equation.

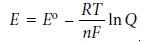
Substituting appropriate values for R and F, assuming a temperature of 25 °C (298 K), and switching from ln to log* gives the potential in volts as

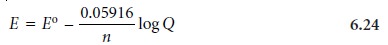
The standard-state electrochemical potential, E°, provides an alternative way of expressing the equilibrium constant for a redox reaction. Since a reaction at equilib- rium has a ∆G of zero, the electrochemical potential, E, also must be zero. Substi- tuting into equation 6.24 and rearranging shows that

Standard-state potentials are generally not tabulated for chemical reactions, but are calculated using the standard-state potentials for the oxidation, E°_ox, and reduction half-reactions, E°_red. By convention, standard-state potentials are only listed for re- duction half-reactions, and E° for a reaction is calculated as

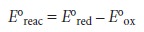
where both E°_red and E°_ox are standard-state reduction potentials.

Since the potential for a single half-reaction cannot be measured, a reference half- reaction is arbitrarily assigned a standard-state potential of zero. All other reduction potentials are reported relative to this reference. The standard half-reaction is

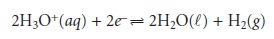
Appendix 3D contains a listing of the standard-state reduction potentials for se- lected species. The more positive the standard-state reduction potential, the more favorable the reduction reaction will be under standard-state conditions. Thus, under standard-state conditions, the reduction of Cu2+ to Cu (E° = +0.3419) is more favorable than the reduction of Zn2+ to Zn (E° = –0.7618).