Doppler effect : Different cases and Applications

Doppler effect

The whistle of a fast moving train appears to increase in pitch as it approaches a stationary observer and it appears to decrease as the train moves away from the observer. This apparent change in frequency was first observed and explained by Doppler in 1845.

The phenomenon of the apparent change in the frequency of sound due to the relative motion between the source of sound and the observer is called Doppler effect.

The apparent frequency due to Doppler effect for different cases can be deduced as follows.

(i) Both source and observer at rest

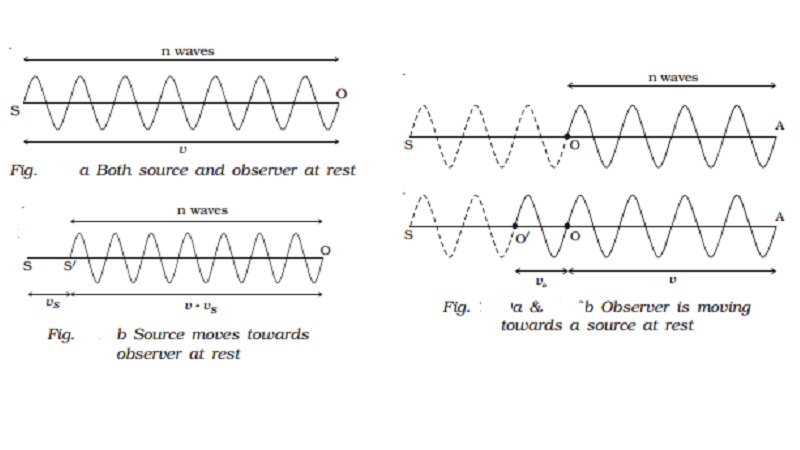
Suppose S and O are the positions of the source and the observer respectively. Let n be the frequency of the sound and v be the velocity of sound. In one second, n waves produced by the source travel a distance SO = v (Fig. a).

The wavelength is λ = v/n

(ii) When the source moves towards the stationary observer

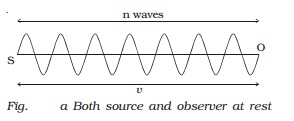
If the source moves with a velocity v_s towards the stationary observer, then after one second, the source will reach S′, such that SS′ = v_s. Now n waves emitted by the source will occupy a distance

of (v?v_s) only as shown in Fig. b.

Therefore the apparent wavelength of the sound is

λ = (v-v_s)/n

The apparent frequency

n? = v/ λ? = (v/v-v_s)n  ????..(1)

As n′ > n, the pitch of the sound appears to increase.

When the source moves away from the stationary observer

If the source moves away from the stationary observer with velocity vs, the apparent frequency will be given by

n? = (v/[v-(-v_s)])n = (v/[v+v_s])n             ????.(2)

As n′ < n, the pitch of the sound appears to decrease.

(iii) Source is at rest and observer in motion

S and O represent the positions of source and observer respectively.

The source S emits n waves per second having a wavelength λ = v/ n .

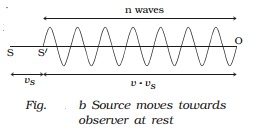
Consider a point A such that OA contains n waves which crosses the ear of the observer in one second (Fig. a). (i.e) when the first wave is at the point A, the nth wave will be at O, where the observer is situated.

When the observer moves towards the stationary source

Suppose the observer is moving towards the stationary source with velocity v_o. After one second the observer will reach the point O′ such that OO′ = v_o. The number of waves crossing the observer will be n waves in the distance OA in addition to the number of waves in the distance OO′ which is equal to v_o/λ as shown in Fig. b.

Therefore, the apparent frequency of sound is

n′ = n + v_o/ λ = n +(v₀/v)n

∴ n′ = ((v+v₀)/v)n ???..(3)

As n′ > n, the pitch of the sound appears to increase.

When the observer moves away from the stationary source

n′ = [v +(-v₀)/v]n

n′ = ( v-v_o / v )n

As n′ < n, the pitch of sound appears to decrease.

Note : If the source and the observer move along the same

direction, the equation for apparent frequency is

n′ = (v-v₀ / v-v_s )n

Suppose the wind is moving with a velocity W in the direction of propagation of sound, the apparent frequency is

n′ = ([v+W-v₀]/ [v+W-v_s])n

Applications of Doppler effect

(i) To measure the speed of an automobile

An electromagnetic wave is emitted by a source attached to a police car. The wave is reflected by a moving vechicle, which acts as a moving source. There is a shift in the frequency of the reflected wave. From the frequency shift using beats, the speeding vehicles are trapped by the police.

(ii)        Tracking a satellite

The frequency of radio waves emitted by a satellite decreases as the satellite passes away from the Earth. The frequency received by the Earth station, combined with a constant frequency generated in the station gives the beat frequency. Using this, a satellite is tracked.

(iii)      RADAR (RADIO DETECTION AND RANGING)

A RADAR sends high frequency radiowaves towards an aeroplane. The reflected waves are detected by the receiver of the radar station. The difference in frequency is used to determine the speed of an aeroplane.

(iv)       SONAR (SOUND NAVIGATION AND RANGING)

Sound waves generated from a ship fitted with SONAR are transmitted in water towards an approaching submarine. The frequency of the reflected waves is measured and hence the speed of the submarine is calculated.