Chapter: 11th Physics : UNIT 10 : Oscillations
Displacement, velocity, acceleration and its graphical representation – SHM
Displacement, velocity, acceleration and its graphical representation – SHM
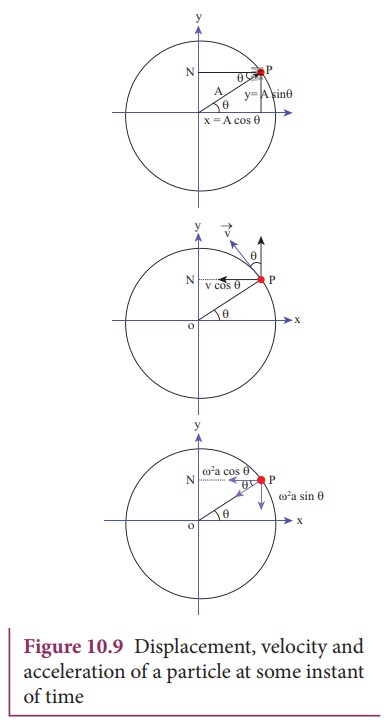
The distance travelled by the vibrating particle at any instant of time t from its mean position is known as displacement. Let P be the position of the particle on a circle of radius A at some instant of time t as shown in Figure 10.9. Then its displacement y at that instant of time t can be derived as follows In ∆OPN
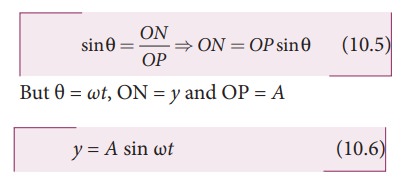
But θ = ωt, ON = y and OP = A
The displacement y takes maximum value (which is equal to A) when sin ωt = 1. This maximum displacement from the mean position is known as amplitude (A) of the vibrating particle. For simple harmonic motion, the amplitude is constant. But, in general, for any motion other than simple harmonic, the amplitude need not be constant, it may vary with time.
Velocity
The rate of change of displacement is velocity. Taking derivative of equation (10.6) with respect to time, we get

For circular motion (of constant radius), amplitude A is a constant and further, for uniform circular motion, angular velocity ω is a constant. Therefore,

From equation (10.6),
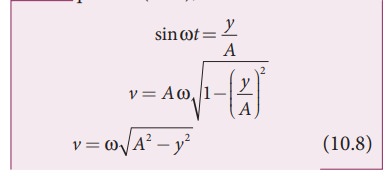
From equation (10.8), when the displacement y = 0, the velocity v = ωA (maximum) and for the maximum displacement y = A, the velocity v = 0 (minimum).
As displacement increases from zero to maximum, the velocity decreases from maximum to zero. This is repeated.
Since velocity is a vector quantity, equation (10.7) can also be deduced by resolving in to components.
Acceleration
The rate of change of velocity is acceleration.
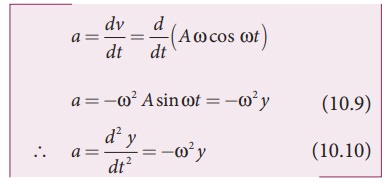
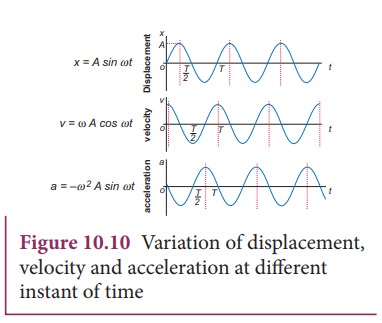
From the Table 10.1 and figure 10.10, we observe that at the mean position

(y = 0), velocity of the particle is maximum but the acceleration of the particle is zero. At the extreme position (y = ±A), the velocity of the particle is zero but the acceleration is maximum ±Aω2 acting in the opposite direction.
EXAMPLE 10.3
Which of the following represent simple harmonic motion?
(i) x = A sin ωt + B cos ωt
(ii) x = A sin ωt+ B cos 2ωt
(iii) x = A eiωt
(iv) x = A ln ωt
Solution
(i) x = A sin ωt + B cos ωt
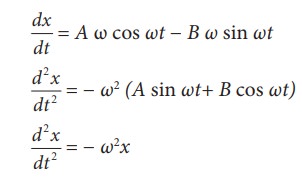
This differential equation is similar to the differential equation of SHM (equation 10.10).
Therefore, x = A sin ωt + B cos ωt represents SHM.
(ii) x =A sin ωt + B cos2ωt

This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.
(iii) x=Aejωt
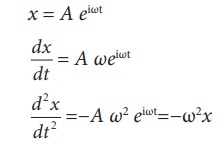
This differential equation is like the differential equation of SHM (equation 10.10). Therefore, x = A eiωt represents SHM.
(iv) x = A ln ωt
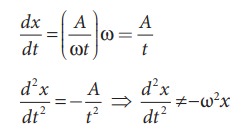
This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A ln ωt does not represent SHM.
EXAMPLE 10.4
Consider a particle undergoing simple harmonic motion. The velocity of the particle at position x1 is v1 and velocity of the particle at position x2 is v2. Show that the ratio of time period and amplitude is
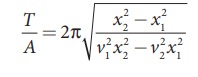
Solution
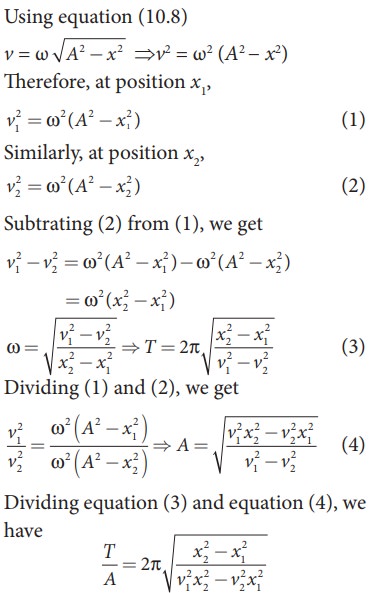
Related Topics